結晶場理論と配位子場理論 - はじめよう固体の科学

更新 2024-2-24

結晶場理論（Crystal field theory）と配位子場理論（Ligand field theory）

金属と配位子

物質は莫大な数の原子によって構成されています．遠くから見ると途方も無い数ですが、近くで見れば一つの原子はいくつか（２〜１０個程度）の原子に囲まれているだけです．いきなりたくさんの原子を考えると大変なので、まずは原子が何個かの原子に囲まれたユニットを抜き出して考えると見通しが良いです．

例として酸化物を考えましょう．酸化物では正の電荷を持つ金属が負の電荷を持つ酸素イオンによって囲まれています（逆もまた然り）．酸化物において物性（磁性、電気伝導性、色など）の主役を担うのは主に金属イオンです．金属イオンが酸素に囲まれたことによってどんな影響が生じるかを見ていきます．

金属イオンを中心に見たとき、周りを囲んでいる酸素のことを配位子と呼びます．この状況は、金属イオンが酸素によって配位されていると言うことができます．ペロブスカイト構造では金属イオンは酸素に八面体配位されており、 $\rm{ZnO}$ では亜鉛イオンは酸素に四面体配位されています．

ｄ電子とエネルギーの分裂

金属イオンの性質を決めるのに最も重要な要素は d軌道の電子です．ｄ電子は金属イオンの種類によって数が異なり、全部で５つの軌道に収納されます．配位子のない状態では５つの軌道は互いにエネルギーが等しい（縮退している）ですが、それぞれ軌道の広がる方向が異なるため、配位子があるとエネルギーにズレが生じて状態が分裂します．

[figure 4] - Diagram Of D Orbitals@clipartmax.com

ｄ軌道がどのように分裂し、電子がどのように分布するかは配位子場理論によって説明されます．

主に考える因子は電子ごとの静電反発であり、この点は原子価殻電子対反発則（VSEPR則）と類似しています．配位子の方向を向いている軌道はエネルギーが高くなり、電子としてはエネルギーの高い軌道には入りたがりません．結果として、d電子が結合電子対とのクーロン反発を最小にするように分布します．

配位子場理論は当初、結晶場理論として定式化され、ｄ電子と配位子の間の静電反発を考慮（配位子は点電荷とみなす）するものでした．一方でVSEPR則の成功の後は、非結合ｄ電子と結合電子対の間の相互作用も併せて考慮することがより好ましいと考えられ、どちらの理論にも同じ考え方が適用されるようになりました．

配位子場理論ではごく簡単な直感的な方法により定性的に正しい状態を導くことができますが、より厳密な分子軌道理論でも同じ結論が得られることが後に示されています．

結晶場理論（Crystal field theory）と配位子場理論（Ligand field theory）
配位子場安定化エネルギー
- 配位子場理論
まとめ
参考文献

八面体配位の場合

金属イオンの d軌道は５重に縮退した軌道ですが、配位子があると金属と配位子との相互作用により d軌道のエネルギー分裂が起こります．配位子場理論では、ｄ軌道と配位子の静電反発を考慮するため、ｄ軌道がどのような方向性を持って空間的に広がっているかを考えることが重要です．

５つのｄ軌道は恣意的に2つの組に分けることができます．

一方は、xyz座標を考えたとき、各平面にあり各軸の間に位置する軌道です（ $d_{xy}, d_{yz}, d_{zx}$ 軌道）．もう一方は、各軸に強い方向性を持った軌道で、x軸・y軸を向いた $d_{x^2－y^2}$ とｚ軸方向を向いた $d_{z^2}$ 軌道があります．

金属イオンの配位子が６つである場合を考えます．VSEPR則によると、配位子が互いに等価な場合は6つの結合電子対の相互反発により八面体配位となります．

xyz座標を考え、配位子を各軸上に配置します．結晶場理論では、金属のｄ電子と配位子の電子とが静電反発することによってｄ軌道の各軌道のエネルギーが変化すると考えます．

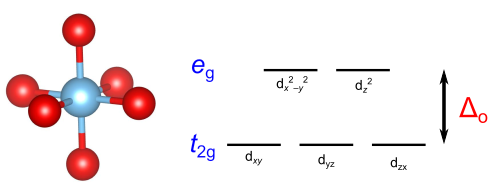
このとき、軸上に位置する $d_{x^2－y^2}$ と $d_{z^2}$ 軌道は配位子の近くにあるため、静電反発によってエネルギーが上昇します．一方、直接的に軸の方向を向いていない $d_{xy}, d_{yz}, d_{zx}$ 軌道は相対的にエネルギーが低下し、ｄ軌道のエネルギー準位が分裂します．

直感的には明らかでないですが、 $d_{xy}$ と $d_{yz}$ と $d_{zx}$ 軌道、 $d_{x^2－y^2}$ と $d_{z^2}$ 軌道はそれぞれエネルギーが等しくなり、結果的にｄ軌道はエネルギーの低い三重縮退の軌道とエネルギーの高い二重縮退の起動に分裂します．前者のエネルギー的に有利な３つの軌道を $t_{2g}$ 軌道（軌道の対称性を表す記号で、tは3重に縮退した状態を表す）、残りの2つを $e_g$ 軌道（eは2重に縮退、ドイツ語のentartet＝縮退に由来）と呼ばれます．

$t_{2g}$ 軌道軌道と $e_g$ 軌道の間のエネルギー差を $Δ_o$ （oはocatahedral のo）と表します． $Δ_o$ の値は、結合電子対が d 電子に与えるクーロン反発力に依存して決まります． $Δ_o$ は分光学的手法で直接測定できる値で、この値が物質の色や電子的性質に大きな影響を与えます．例えば、ルビーやサファイアなどの宝石の色は $Δ_o$ の影響によるものです．

$Δ_o$ は配位子の種類によって大きく変わります．酸化物では配位子は酸素イオンだけですが、世の中には窒素イオンや分子イオンなど様々な配位子が存在します．配位子の電気陰性度が大きい場合、結合電子対の電荷中心は配位子近くに偏ります．ゆえに、配位子の電気陰性度が高くなると d 電子への静電的な影響が減少し、 $Δ_o$ が小さくなります．

配位子による $Δ_o$ の大きさへの影響の差異は分光学的系列として知られ、例えば以下のような傾向があります．

$\rm{CO \gt CN^- \gt PR_3 \gt NH_3 \gt H_2O \gt OH^- \gt F^- \gt Cl^- \gt S^{2-} \gt Br^- \gt I^-}$

ｄ軌道の電子は、 $t_{2g}$ 軌道と $e_g$ 軌道に分裂した軌道に対し、エネルギーの低い軌道（ $t_{2g}$ 軌道）から順番に占有します．電子はスピンの自由度があるので、アップスピンとダウンスピンは別の状態とみなされ、一つの軌道あたりスピンの異なる２つの電子が入ることができます．１つ目の電子は $t_{2g}$ 軌道のうちの一つの軌道を占めます．

２つ目の電子の場合には、 $t_{2g}$ 軌道のうち既に占有された軌道に逆方向のスピンを持って入るか、 $t_{2g}$ 軌道でまだ占有されていない軌道を占めるかの２つの選択肢があります．実際は、２つ目の電子は $t_{2g}$ 軌道の空の軌道に入り、スピンは１つ目の電子と平行に配置されます（フントの規則）．

これは、1つの軌道で電子を対にするには2つの電子の間の静電反発を克服する必要があるためです．すでに占有されている軌道に2個目の電子を入れるにはエネルギーが必要で、このエネルギーを電子対生成エネルギー $P$ と言います．

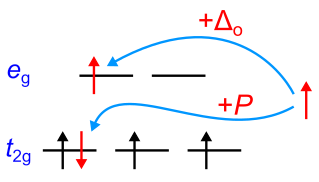
３つ目のｄ電子は２つ目の電子と同様に $t_{2g}$ 軌道に入りますが、４つ目の電子の配置には再び2つの選択肢があります． $t_{2g}$ 軌道に、既に占有している電子と反対方向のスピンを持って入るか、あるいは $e_g$ 軌道に入るかを選びます．どちらが実現するかは $Δ_o$ と $P$ のエネルギー差によって決まります．

$Δ_o \gt P$ ならば $e_g$ 軌道に入り、4つの電子はすべて平行なスピンを持つことになります． $Δ_o \lt P$ の場合、 $e_g$ 軌道を空け、 $t_{2g}$ 軌道に４つ目の電子として入ります．前者のケースをハイスピン（高スピン）、後者のケースをロースピン（低スピン）と呼びます．

そして、５つ目以降のｄ電子は高スピンか低スピンのケースによって軌道への入り方が異なります．９，１０番目の電子には入る軌道の選択肢がなくなり、いずれも $e_g$ 軌道を占めます．

特定の電子数の時は、静電反発を抑えるためにさらに配位構造が歪み、軌道もそれに合わせて分裂することで全体のエネルギーを下げます．この現象はヤーンテラー効果と呼ばれており、多くの物質で見られます．

四面体配位の場合

四面体配位の場合、原子の4つの配位子は、立方体の８つの頂点のうち４つの頂点に配置していると考えることができます．八面体のケースと比べると想像しにくいですが、立方体の辺を向いている $d_{xy}$ と $d_{yz}$ と $d_{zx}$ 軌道（ $t_2$ 軌道）は、面方向を向いている $d_{x^2－y^2}$ と $d_{z^2}$ 軌道（ $e$ 軌道）よりも結合電子対に近い位置に位置します．

その結果 $t_2$ 軌道は $e$ 軌道よりも大きな静電反発を受けてエネルギー的に高くなり、その順序は八面体配位の場合と逆になります．ただし、配位子と軌道が完全に同じ方向を向いていた八面体配位のケースよりはエネルギー差が小さくなり、 $Δ_t$ （tはtetrahedra のt）は $Δ_o$ の 4/9 程度の値をとることが知られています．

$Δ_o$ は小さいためスピン対形成エネルギー $P$ よりも小さいケースが主で、それゆえ四面体配位では高スピンとなります．

四面体配位の場合もヤーンテラー効果が働き、配位構造が歪む場合があります．

正方形配位の場合

正方形配位は一部の錯体や酸化物で見られます．正方形配位は、八面体配位でｚ軸方向の配位子が無限の彼方へ行ってしまった場合とみなすことができます．このため、ｚ方向を向いているｄ軌道の静電反発が小さくなり、エネルギーが低くなります． $d_{x^2－y^2}$ 軌道だけ相変わらず配位子と強く静電反発をしており、それゆえ最も高いエネルギーを持ちます．

結果として、エネルギーは以下の順番になります．

　　 $d_{x^2－y^2}$ 軌道 > $d_{xy}$ 軌道 > $d_{z^2}$ 軌道 > $d_{yz}$ と $d_{zx}$ 軌道

特に $d^8$ の電子配置をとるときに正方形配位が安定化されることが知られています．その他に、銅（ $d^9$ ）、ニッケル（ $d^9$ ）、鉄（ $d^6$ ）の平面四配位の物質が報告されています．

リンク

配位子場安定化エネルギー

配位子が中心金属イオンに近づくと、次のような事が起こると考えられます．

・配位子と金属イオンの共有結合の形成によるエネルギー低下
・結合電子対の相互反発と、配位子間の反発によるエネルギー上昇
・結合電子対が中心原子の非結合電子に及ぼす反発によるエネルギー上昇

配位子場理論では、主に最後の寄与を考えます．この場合、中心原子の電子が球状に分布していれば、配位子の幾何学的分布は関係なく、反発エネルギーは常に同じになります．

しかし、一般のｄ電子数の場合はそうではなく、電子がどの軌道にどの向きで入るかによってエネルギーが異なります．ｄ電子がどの配置をとる時に最もエネルギー的に安定化されるかを考える指標として、配位子場安定化エネルギー（LFSE）が使用されます．

これは、ｄ電子が球状に分布している場合に想定される静電反発エネルギーと、ある電子配置をとるときのｄ電子と結合電子の間の静電反発エネルギーとの差として定義されます．金属イオンはなるべく、LFSEの大きな電子配置をとろうとします．

例えば、八面体配位では $t_{2g}$ 軌道のエネルギーが低く、 $t_{2g}$ 軌道を優先的に占めることで全体のエネルギーが低下します．また、高スピンか低スピンによって全体のエネルギーが決まりますが、これはｄ電子の数によってLFSEの値が変わります．

配位子場理論

結晶場理論は、金属のd電子と配位子の結合電子との間の静電反発を考慮したものです．VSEPR則と同様、簡単な直感的な描写から定性的に正しい結論を与えることができるので非常に有用ですが、限界もあります．

原子と原子の間で相互作用をする場合、静電作用だけでなく、原子どうしの軌道が重なり合うことで共有結合を形成します．このとき、エネルギー的に安定な結合性軌道と不安定な反結合性軌道ができ、結合性分子軌道に電子を収容することにより結合ができます．

結晶中の金属イオンにおいても同様に、金属と配位子の軌道から結合性軌道が形成され、その軌道に配位子の電子を収容することにより結合が構築されます．

分子軌道法によって記述する方法は配位子場理論と呼ばれます．配位子による相互作用を分子軌道法に従って記述する方法は配位子場理論と呼ばれます．

リンク

まとめ

物質中では多数の原子が複雑に分布していますが、ローカルなスケールでは原子が数個の他の原子に配位されているというシンプルな描写が成り立ちます．

金属イオンにアニオンが配位している場合が典型であり、この配位の影響により物質は多様な電子・光学物性を示します．金属がアニオンに配位された分子がネットワークを形成することで固体が出来上がるので、固体の物性はまず小さな分子を考えてみることから始まります．

参考文献

U. Müller, Inorganic Structural Chemistry (Wiley, 2007).

化学と教育 2017 年 65 巻 4 号 p. 198-201

結晶構造の描画にはVESTAを使用．K. Momma and F. Izumi, "VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data," J. Appl. Crystallogr., 44, 1272-1276 (2011).