更新 2024-3-2
ホイスラー合金(Heusler alloy)
鉄は脆く錆びやすいですが、炭素を加えると硬く丈夫な鋼鉄ができます.クロムやニッケルを加えると錆びにくいステンレス鋼ができます.組み合わせることは個々の特性を加えるだけでなく、時に思いもよらない結果をもたらすのです.
1903年に Fritz Heuslerが発見した合金は不思議な物質でした.原料はといずれも磁石ではないにも関わらず、組み合わせた合金
は磁石の性質を示したのです.同様に
を
や
に置換した材料も磁石となる事が分かりました.もちろん、
も
も磁石ではありません.
に関する研究は息子のOtto Heuslerに引き継がれ、1934年に結晶構造が明らかにされました.その後、
と同様の結晶構造を持つ物質は無数に存在し、組成によって制御可能な千差万別の物性・機能性を持つ材料であることが明かされたのです.
ホイスラー合金と呼ばれるこれらの物質は、今日では1000種類を超える組成が報告されています.磁性材料、電子材料、熱電材料として注目される物質も多く、実用化もされています.
今回は、ホイスラー合金の成立と構造、機能を見ていきます.類似の物質群であるハーフホイスラー合金とNowotny-Juza-Phase、正方晶ホイスラー合金についても触れていきます.
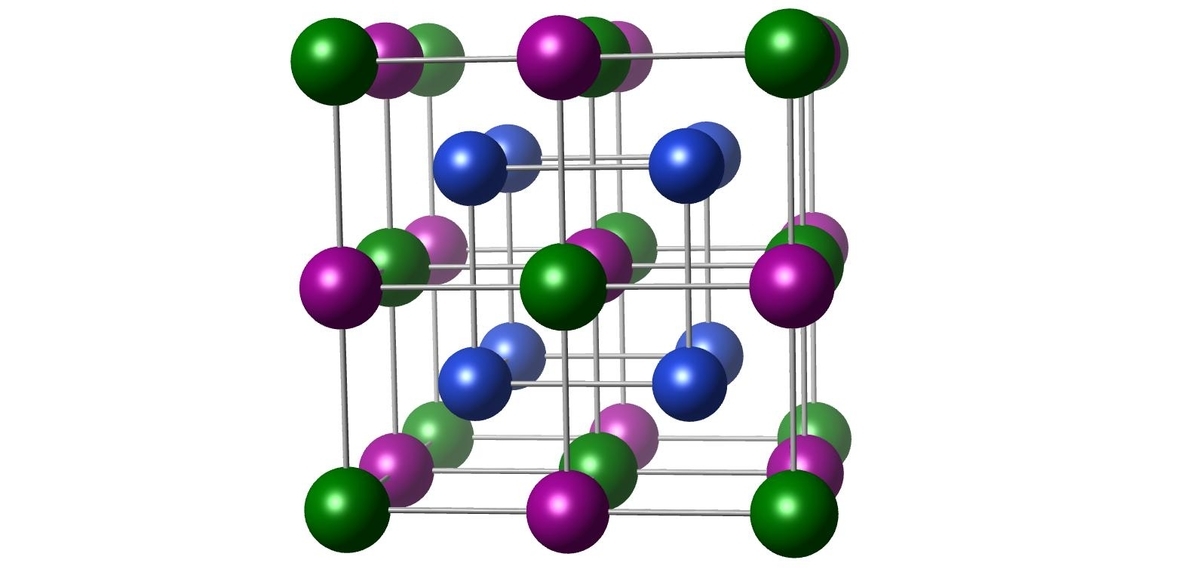
ホイスラー合金の結晶構造
ホイスラー合金は一般式で表される組成を持つ金属間化合物です.
と
には比較的電気的に陽性な遷移金属、
には比較的電気的に陰性な典型元素が入ります.
はランタノイドやアルカリ土類金属である場合もあります.
ホイスラー合金の結晶構造は比較的シンプルです.面心立方構造を基調とし、有名な型構造や
型構造とも類似性を持ちます.
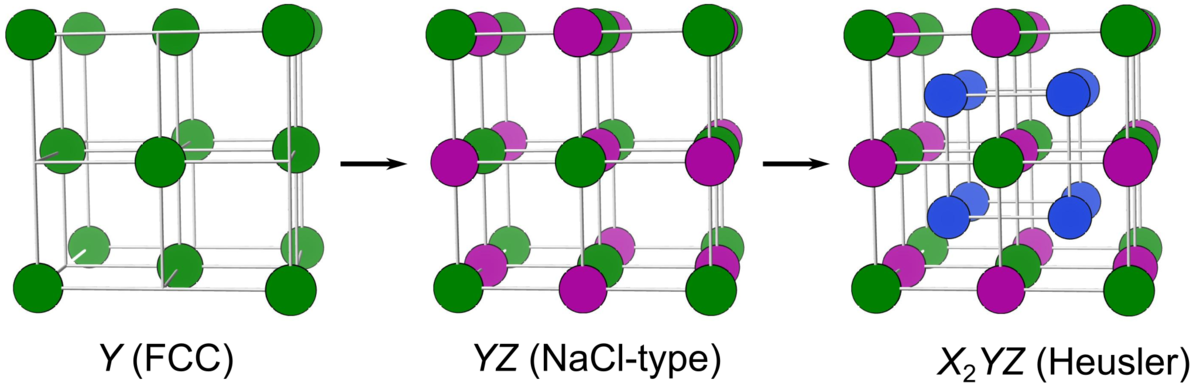
の面心立方構造を考えます.面心立方構造の八面体間隙に
を入れると、
型構造の
が生成します.続いて、面心立方格子の四面体間隙全てに
を入れるとホイスラー合金
が完成します.
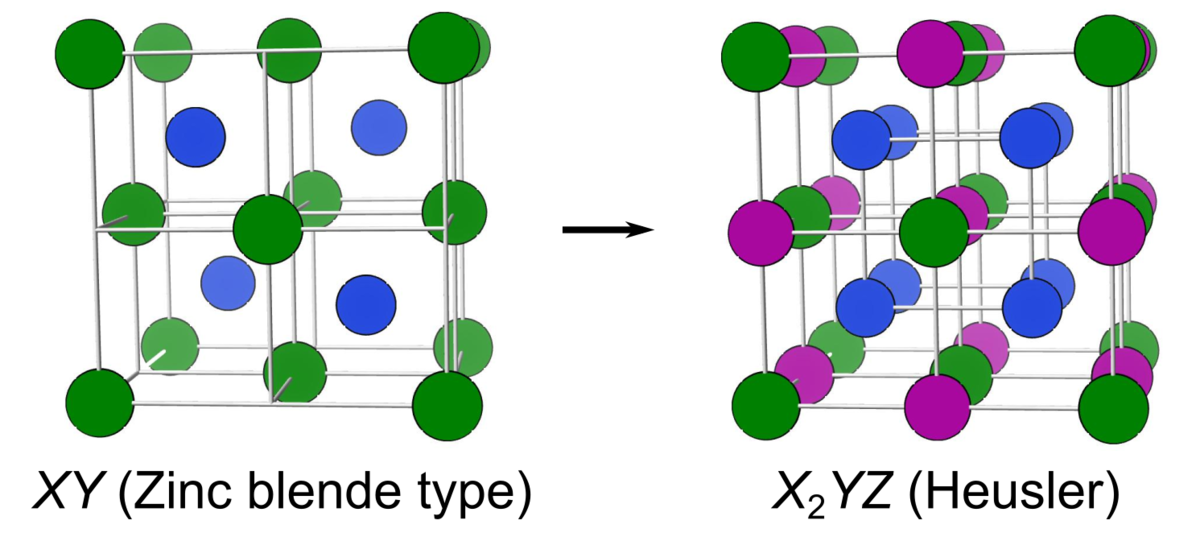
あるいは、からなる閃亜鉛鉱型構造を考えます.
を四面体間隙、
を八面体間隙に入れることによってもホイスラー合金となります.
場合によっては、型構造を出発点に考えることもあります.
および
からなる
型の構造ユニットを考え、これらが互いに
型構造をとるように配列させることでホイスラー合金の構造となります.
ホイスラー合金の構造はシンプルゆえ、以上のように様々な表し方があります.また、ホイスラー合金の構造を縦に引き伸ばしたような構造をもつ正方晶ホイスラー合金も近年活発に研究されています.
ハーフホイスラー構造
ハーフホイスラー合金は、その名の通りの数が半分になったホイスラー合金です一般式は
で表されます.ホイスラー合金の構造から
を、残された
がダイヤモンド構造となるように取り除くことでハーフホイスラーとなります.
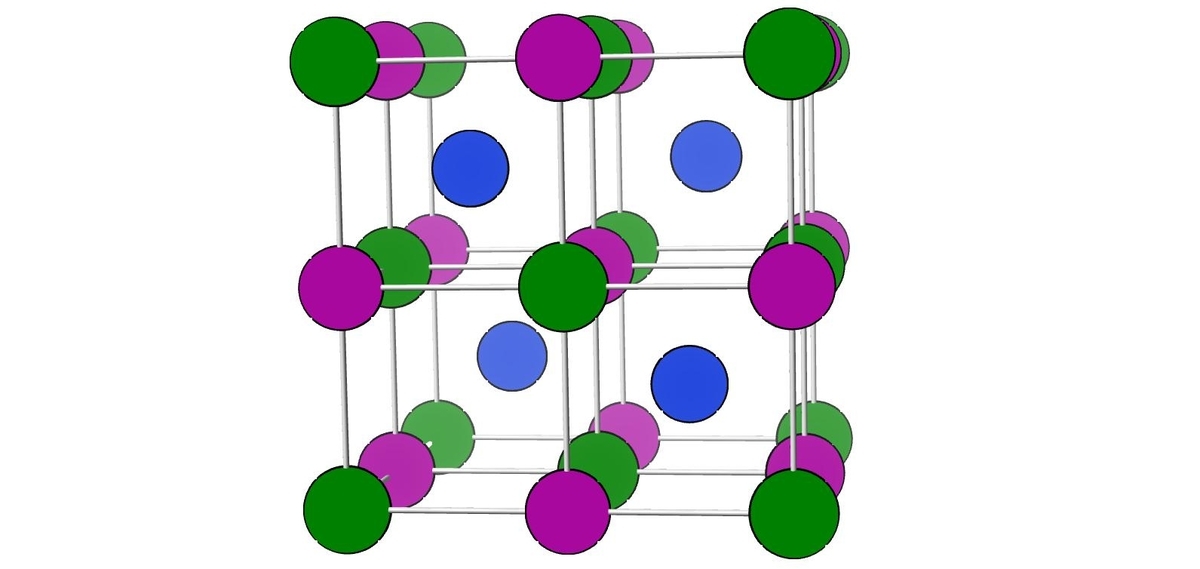
あるいは、からなる閃亜鉛鉱型構造の八面体間隙に
を入れ込んだ構造であるとも考えることが出来ます.
ホイスラー合金と電子数
物質の性質は、構成元素の価電子数によって大きく影響を受けます.シンプルな二元系の物質でも、金属になるものもあればバンドギャップを持つ半導体(あるいは絶縁体)となるものもあります.
二元系の半導体材料にはなどの材料がありますが、これらの共通点はいずれも価電子数の合計が8となることです.この規則はオクテット則と呼ばれ、各半導体はⅢ-Ⅴ、Ⅳ-Ⅳ、Ⅱ-Ⅵ半導体のように呼ばれます.オクテット則が成り立つ物質は金属にならずに半導体(絶縁体)となるケースが多いです.
同様のルールはホイスラー合金やハーフホイスラー合金でも確認されています.典型元素のみから構成される三元系ではオクテット則が成り立つ物質が多くあります.
特に、や
のように価電子数が1-2-5の組み合わせである系はNowotny-Juza-Phaseと呼ばれ、ワイドギャップ半導体として知られています.名前はついていないですが、価電子数の組み合わせが1-3-4(
など)や2-2-4(
)のような例もあります.
ハーフホイスラー合金では、遷移金属が加わるためオクテット則を満たすには電子数が多すぎますが、代わって18電子則が有効な指針となります.の組成において、電気的に陽性な
が価電子を
と
に受け渡し、
が
、
が
になった際に特に安定になるとされます.
例として、(4-9-5)や
(4-10-4)が挙げられます.このとき、価電子数は合計で18であり、有限のバンドギャップを持ちます.
二種類以上の遷移金属を含むホイスラー合金では24電子則が知られています.すなわち、(8-8-5-3)のように24個の価電子を持つ化合物が半導体になることが見いだされています.
以上の規則から外れる電子数を持つ物質は磁性を示すか、金属になるか、別の結晶構造となる傾向が強くなります.
ホイスラー合金の性質
ホイスラー合金およびハーフホイスラー合金は組成の選択肢が非常に豊富で、それゆえ無数の物質が知られています.それらは電子数に応じて様々な機能を示します.
以下では、ホイスラー合金の主な機能のうち、磁気物性と電子物性について見ていきます.
磁性
強磁性
最初に発見されたホイスラー合金であるが、強磁性金属を含まないにも関わらず強磁性を示します.ホイスラー合金の強磁性転移温度は組成によって大きく変わり、200 Kから1200 Kにまで及びます.
ホイスラー合金の飽和磁気モーメントの値は価電子数によって左右されます.上述のように、ハーフホイスラー合金に18電子則、ホイスラー合金には24電子則が知られているわけですが、この閾値を価電子数を越えた分だけ磁気モーメントが大きくなります(Slater-Pauling則).
ハーフメタル(Half metal)
ホイスラー合金は、1983年にや
がハーフメタルであることが予言されたことで、物性物理の界隈で注目を浴びました.
電子は磁石の性質を持ち、上向きと下向きの2つの状態をとります.ハーフメタルでは、一方のスピンは金属のように伝導するのに対し、もう一方の電子は伝導できません.この性質は、スピンの自由度を駆使するスピントロニクスにとって垂涎の性質であり、実際にスピン注入や磁気トンネルデバイス用途で使用されています.
磁化補償されたフェリ磁性(Compensated ferrimagnet)
一方のスピンしか流さないハーフメタルは有用ですが、大きな磁化を持つ場合が多く、迷走磁場を発生させやすく外部磁場の影響を受けやすいという問題が生じます.このため、可能ならば磁化は小さい、あるいはゼロであるほうが望ましいとされます.
隣り合う原子の磁気モーメントが逆方向に向くことで正味の磁化をゼロにしたハーフメタルを磁化補償されたフェリ磁性体(長ったらしい)と呼び、実際に薄膜や
などで報告されています.
スピンギャップレス半導体(Spin-gapless Semiconductors)
ギャップレス半導体とはバンドギャップがゼロの半導体(それは半導体なのかはさておき)ですが、スピンギャップレス半導体とは一方のスピンに関してのみバンドギャップがあり、もう一方についてはゼロギャップの半導体です.電荷の担い手である電子と正孔がどちらも一方のスピン状態であるため、半導体スピントロニクスへの応用が期待されています.
lは、実際にスピンギャップレス半導体であることが報告されたホイスラー合金です.
超伝導
ホイスラー合金の中には、超伝導を示すものも知られています.1982年、や
(
はレアアース)が超伝導を示すことが発見されました.現在に至るまでホイスラー合金の超伝導体はそれなりに見つかっていますが、数十ケルビンクラスの高い転移温度を示すものは見つかっていません.
超伝導は27個の価電子を持つホイスラー化合物に多く見られます.バンド構造計算により、27の価電子を持つ系では伝導に寄与できる電子の数が非常に多くなり、それゆえ超伝導に有利であるとされます.(専門的に言えば、van Hove 特異点によってフェルミエネルギー近傍の状態密度が非常に大きくなること.)
ハーフホイスラー合金では超伝導は珍しいですが、や
、その類縁物質で見られます.
熱電材料
熱を電気エネルギーに変換可能な熱電材料は、排熱を有効活用する手段として注目されており、電気をよく流すが熱を流さない半導体材料が理想とされています.18電子則を満たすハーフホイスラー合金は半導体的な挙動を示し、バンドギャップが調節可能なことから熱電材料として有望です.
ハーフホイスラー合金は優れた熱電特性を示す事が予言され、実際に高いゼーベック係数と高い電気伝導度を示すことが実証されました.一方で、熱伝導率は比較的高いとされています.近年ではn型のやp型の
の研究が活発であり、熱電性能指数ZTは最高で1.6にまで達しています.
トポロジカル材料
近年、物性物理の世界ではトポロジーの概念を様々な物質系に応用することが盛んに行われています. 量子井戸構造で量子スピンホール効果状態が実現したことを皮切りに、
や
と似た結晶構造を持つハーフホイスラー合金にも注目が集まりました.
ハーフホイスラー合金はバンドギャップが組成によって調節可能であることから、トポロジー的に非自明な状態(電子構造がメビウスの輪のように捻れていること)を実現可能であるとの指摘がありました.実際、非自明な電子構造に加えて、反強磁性()や超伝導(
)、重い電子系(
)のような興味深い物性が共存する物質が見出されています.
顕著な例として、や
、
などが、Weyl粒子と呼ばれる質量のない電子を持つWeyl半金属状態と磁性が共存したエキゾチックな状態であることが発表されました.
まとめ
ホイスラー合金は長い歴史を持ち、莫大な研究がされながらも、現在でも魅力的な新物性が続々と見出されています.ホイスラー合金は組成の自由度が非常に高く、それゆえ物性の制御が容易に行なえます.
驚くべきことは、こうした多様な物性が価電子数という単純な概念によって見事に整理されることであり、新しい物質・物性の予言にも役立ちます.こうした特性は熱電材料やトポロジカル材料のように微妙な物性制御がカギになる分野において重宝されます.
これまでのホイスラー合金の物性開拓は物理分野に偏重していましたが、形状記憶合金や触媒としての用途もあります.今後も幅広い分野でホイスラー合金が活用されていくことが期待されます.
参考文献
Progress in solid state chemistry, 2011, 39.1: 1-50.
Annual Review of Materials Research, 2017, 47: 247-270.
Applied Physics Letters, 2021, 118.14: 140503.
Science and technology of advanced materials, 2021, 22.1: 235-271.
磁性
Physical Review Letters, 1983, 50.25: 2024.
Physical Review B, 1983, 28.4: 1745.
Physical review letters, 2014, 112.2: 027201.
Physical Review B, 2017, 95.6: 060410.
Physical review letters, 2013, 110.10: 100401.
超伝導
Buckel and W. Weber, Kernforschungszentrum Karlsruhe, Germany, 1982.
熱電
Journal of electronic materials, 2009, 38.7: 934-939.
Journal of Applied Physics, 2009, 105.1: 013709.
Advanced Energy Materials, 2018, 8.1: 1701313.
トポロジカル
Physical Review B, 2012, 85.1: 012405.
Nature materials, 2016, 15.11: 1161-1165.
Nature Physics, 2018, 14.11: 1119-1124.
その他の物性
Applied Physics Letters, 1996, 69.13: 1966-1968.
Science advances, 2018, 4.10: eaat6063.
結晶構造の描画にはVESTAを使用.K. Momma and F. Izumi, "VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data," J. Appl. Crystallogr., 44, 1272-1276 (2011).