最密充填と結晶構造
金属単体のほとんどは面心立方構造(立方最密構造、fcc)、六方最密構造(hcp)、体心立方構造(bcc)のいずれかの結晶構造を持ちます.いずれも非常にシンプルかつ対称性が高く、容易に理解できます.しかし、単体から化合物になって二元系、三元系と原子の種類が増えていくと、結晶構造はどんどん複雑になります.
しかし、ポーリングが「結晶中に含まれる本質的に異なる種類の成分の数は少ない傾向にある」と言ったように、結晶構造はいたずらに複雑にはなりません.一見して複雑な構造であっても、部分部分をよく見れば、必ずシンプルな結晶構造から組み立てることができるようになっています.*1
結晶構造を考えるにあたって、2つの方法があると思っています.一つは多面体に注目する方法、もう一つは充填パターンに注目する方法です.多面体に注目する方法は以前に紹介したので、今回は充填パターンに着目して結晶構造を見ていきます.

スタート地点になるのは2つの最密充填(六方最密、立方最密)構造と体心立方構造です.最密充填とはいっても全ての空間が埋まっているわけではなく、充填率は74%程度しかありません.ゆえに、どんな充填パターンにも必ず隙間(間隙)が存在し、この隙間に別の原子を入れることで新しい結晶構造が得られます.
また、一種類の原子から構成される結晶構造の一部を別種類の原子または構造ブロックで置き換えることによっても新しい結晶構造が出来上がります.
今回は、基本的な結晶構造からどのようにして複雑な結晶構造を得られるのかを見ていきます.
方針
基本的な結晶構造からスタートして、以下の方法によって結晶構造がどのようにできあがるかを見ていきます.
(1)間隙に別種の原子、または構造ブロックを入れる(Fill)
(2)原子の一部を別種の原子、または構造ブロックで置き換える(Substitute)
(3)上記の組み合わせ(Fill + Substitute)
それぞれの言葉の意味はおいおい明らかになることでしょう.
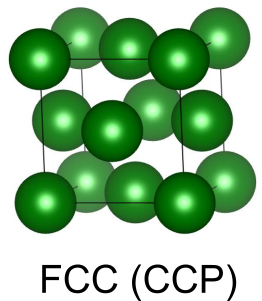
面心立方構造(立方最密構造、fcc)
という原子からなる面心立方構造を考えます.
面心立方構造には単位胞あたり4つの原子が含まれます.最密充填層を ABCABC… の順に積層することで面心立方構造が得られ、各原子は12個の原子に囲まれています.
面心立方構造の単位胞には、4つの八面体間隙と8つの四面体間隙があり、四面体間隙のうち、半数は上向き、もう半数は下向きの四面体です.以下では八面体間隙を Oct、上向きの四面体間隙を Tet1、下向きの四面体間隙を Tet2 と呼びます.
(1)Fill
まずは、間隙にと同じ種類の原子を入れる場合を考えましょう.
Oct に原子を入れると、単純立方構造が得られます.その名の通り、単純な立方体の構造です.一方、Tet1 か Tet2 のいずれかに原子
を入れるとダイヤモンド構造が得られます.Tet1 か Tet2 の両方に入れた場合は体心立方構造となります.
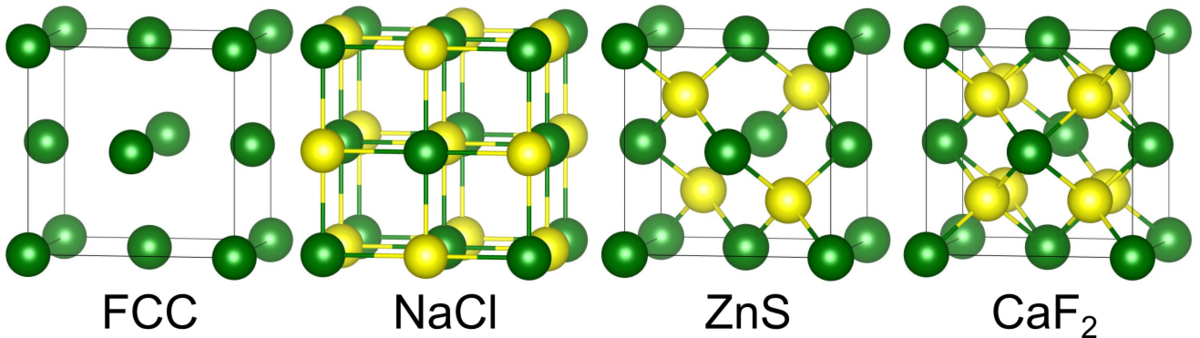
もし異なる原子を入れていた場合はどうなるでしょう.
Oct に原子を入れると、有名な
型(岩塩型)構造となります.この際、
は
に八面体配位され、
も
に八面体配位されています.
一方、Tet1 か Tet2 のいずれかに原子を入れると閃亜鉛(
)型構造に、両方に原子
を入れると蛍石型(
型)構造となります.Tet1 の半分に原子
が入り、原子
が体心立方構造を形成しているのが
型構造です.
さらに別の種類の原子を加えます.
Oct にを入れた状態で、Tet1 か Tet2 の両方に原子
を入れるとホイスラー合金で有名なホイスラー構造が得られます.Tet1 か Tet2 のどちらかにしか原子
を入れない場合はハーフホイスラー構造と呼ばれます.
続いて、面心立方構造の間隙に別の構造ブロックを入れてみます.「構造ブロック」とは、二原子分子や四面体分子のような「形」を持った一塊のユニットです.例えば、面心立方構造の Oct に2原子分子を入れるとパイライト型(型)構造が得られます.
(2)Substitute
面心立方構造の一部を異なる原子で置き換えます.
原子からなる結晶構造のどこを原子
で置き換えるのかが問題になりますが、簡単のため最密充填層を取り出して考えます.
と
の比が1:1の場合、
と
を順番に並べると
型構造となります.
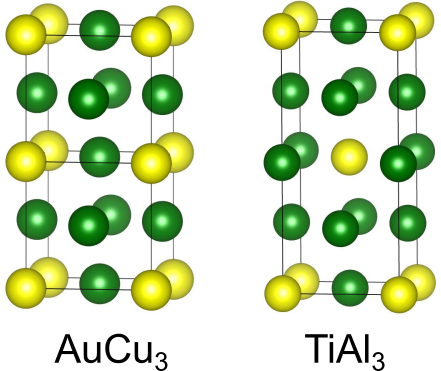
と
の比が1:3の場合、下図のように原子を並べることで
型構造および
型構造が得られます.特に
型構造は重要で、Oct の一部に原子
を入れることでペロブスカイト型構造が得られます.
(3)Fill + Substitute
上記2つの操作を組み合わせた応用編です.
操作(1)で得られた型構造の一部を、操作(2)によって別種原子で置き換えます.
サイトを1:1の組成比で別の原子に置き換えると、置き換えのパターンによって
型構造と
型構造が得られます.さらに、異なる組成比では、
型、
型、
型構造などが導けます.
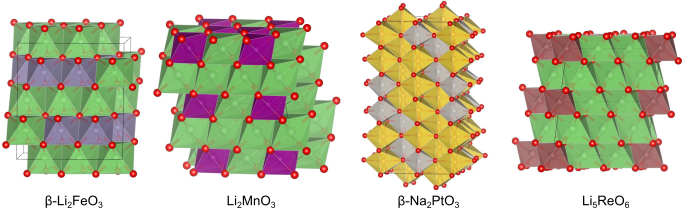
別種原子で置き換える代わりに、対応するサイトから原子を取り除くことによっても新しい結晶構造となります.型構造と
型構造から1種類の原子サイトをすべて取り除くことで得られるのが、それぞれ
型と
型構造です.
蛍石型の金属サイトの半分を別の原子で置き換えることでパイロクロア型構造が得られます.パイロクロア型構造のサイトを適当に並び替えることによりβ-パイロクロア型構造となります.
また、(1)で得られたダイヤモンド構造の一部を別種原子で置き換えることで、型構造が得られます.
六方最密構造(hcp)
という原子からなる六方最密構造を同様に考えます.
六方最密構造には単位胞あたり2つの原子が含まれます.最密充填層を ABAB… の順に積層することで六方最密構造が得られ、各原子は12個の原子に囲まれています.
面心立方構造の単位胞には、4つの八面体間隙と8つの四面体間隙があります.四面体間隙のうち、半数は上向き、もう半数は下向きの四面体です.同様に、八面体間隙をOct、上向きの四面体間隙を Tet1、下向きの四面体間隙を Tet2 と呼びます.

(1)Fill
間隙にと同じ種類の原子を入れる場合を考えます.
Oct に原子を入れると、二重六方最密構造(日本語に定訳がないですがdouble hcpのこと)ができ、最密充填層が ABACABAC… の構造になります.ランタンやネオジムの結晶構造として知られます.Tet1 か Tet2 のいずれかに原子
を入れた結晶構造を持つ物質は稀ですが、超高圧化のダイヤモンドがこの構造をとるらしいです.
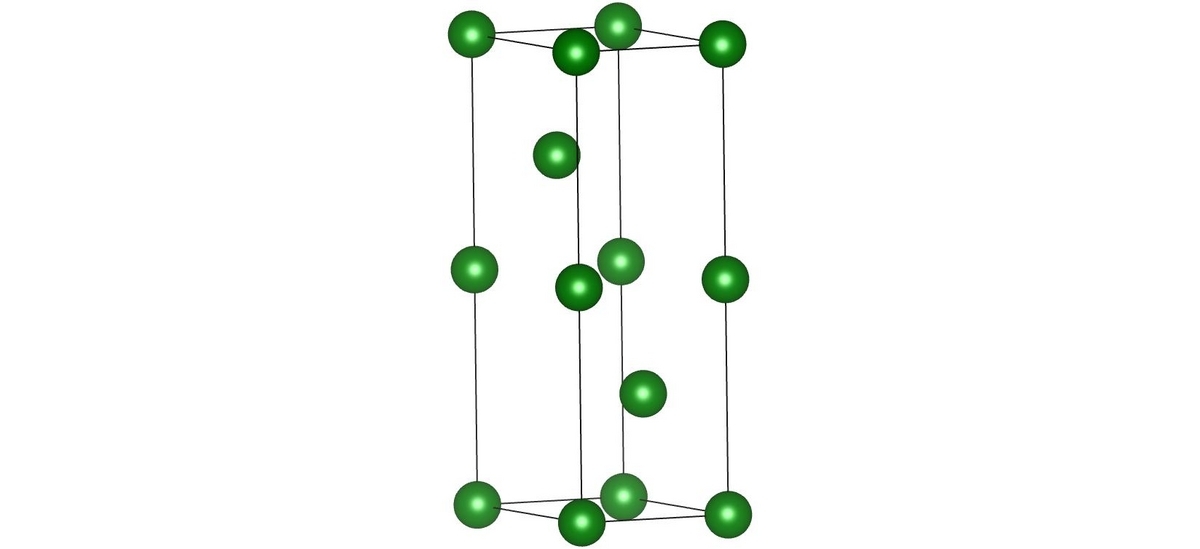
続いて、異なる原子を入れた場合を考えます.
Oct に原子を入れると、
型構造となります.立方最密構造の八面体サイトに原子を入れた
型構造の親戚と呼べる構造です.ただし、
型では
は
に八面体配位されていますが、
は
に三角柱型に配位されています.
Oct に原子を入れ、Tet1 か Tet2 のいずれかに原子
を入れるとウルツ鉱型構造となります.
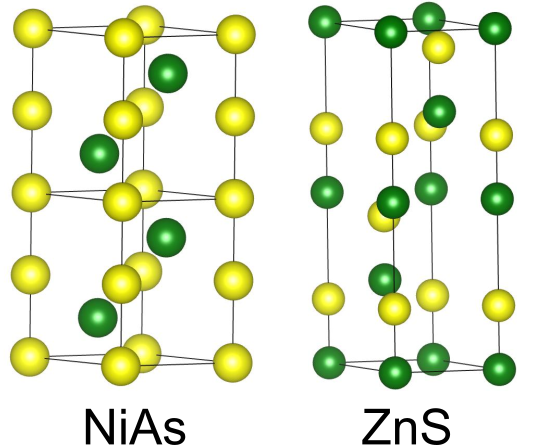
(2)Substitute
六方最密構造の一部を異なる原子で置き換えます.
立方最密構造の際と同様に最密充填層を取り出して考えます.と
の比が1:1の場合は
型構造が、
と
の比が1:3の場合、
型構造および
型構造が得られます.
六方最密構造の最密充填層を一層取り除けば、単純六方格子となります.
(3)Fill + Substitute
操作(1)で得られた型構造の一部を、操作(2)によって別種原子で置き換えます.
サイトを1:1の組成比で別の原子に置き換えると、
型構造となります.ここでは
と
が層状に秩序化しています.
別の原子で置き換える代わりに、対応するサイトから原子を取り除くと、型構造が得られます.
型構造は
型構造とよく似ており、遷移金属ダイカルコゲナイド(TMD)として有名です.また、
型構造から
サイトの半分を取り除くとき、空孔のパターンによっては
型構造となります.
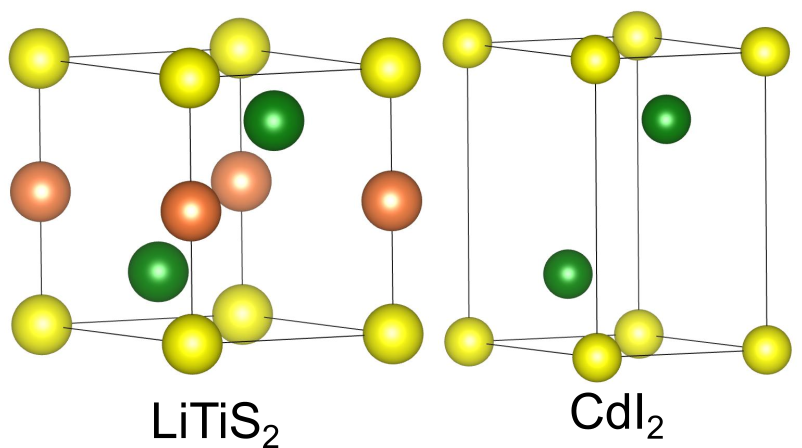
型構造の
サイトの1/3を取り除き
がハニカム格子を組むように配置すると、コランダムで有名な
型構造が現れます.
型の
サイトに金属を二種類配置させればイルメナイト型および
型構造となります.
型構造では
が
に三角柱型に配位されていますが、もう一つの三角柱にも
を入れたのが
型構造です.超伝導体の
が有名です.
型構造から派生して、
型、
型、
型などの結晶構造が導かれます.
体心立方構造(bcc)
最後に、という原子からなる体心立方構造を同様に考えます.
体心立方構造には単位胞あたり2つの原子が含まれます.最密充填ではありませんが、多くの金属で見かける結晶構造です.各原子は8個の原子に囲まれています.
面心立方構造の単位胞には、6つの八面体間隙と12の四面体間隙があります.八面体間隙をOct、四面体間隙を Tet と呼びます.
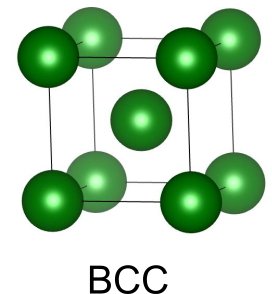
(1)Fill
体心立方構造には間隙が多くあり、金属の水素化物ではこの間隙サイトに水素が入り込みます.などが該当します.
Oct に二原子を同時に挿入すると、二原子の向きによってルチル型構造とマーカサイト型構造が得られます.超伝導体で有名なA15型構造も同様の手順で導かれます.
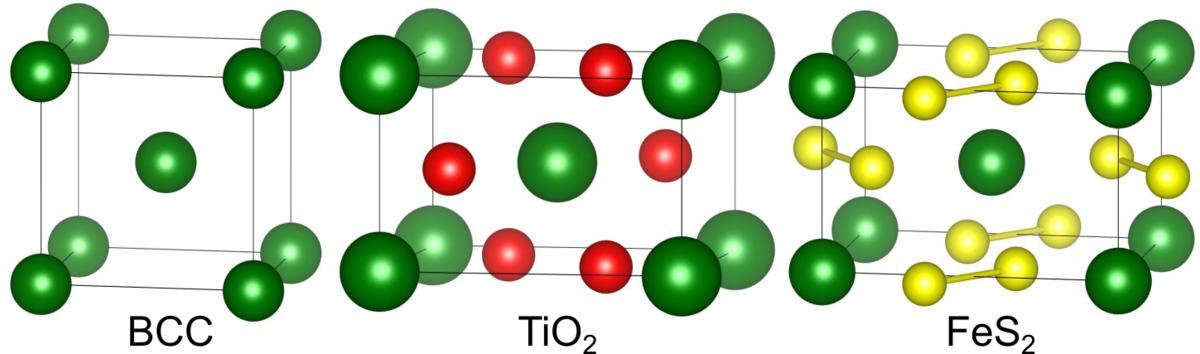
(2)Substitute
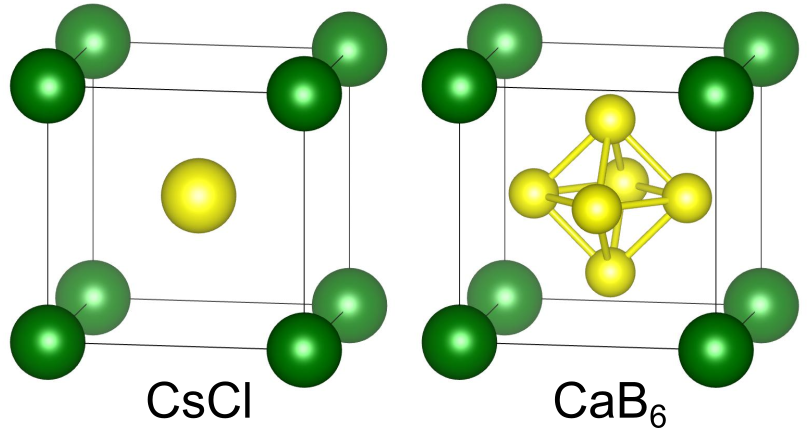
体心立方構造の一部を異なる原子で置き換えた構造で最も有名なのは、体心サイトを
で置き換えることによってできる
型構造です.原子
の代わりに
からなる八面体で置き換えれば、
型構造となります.
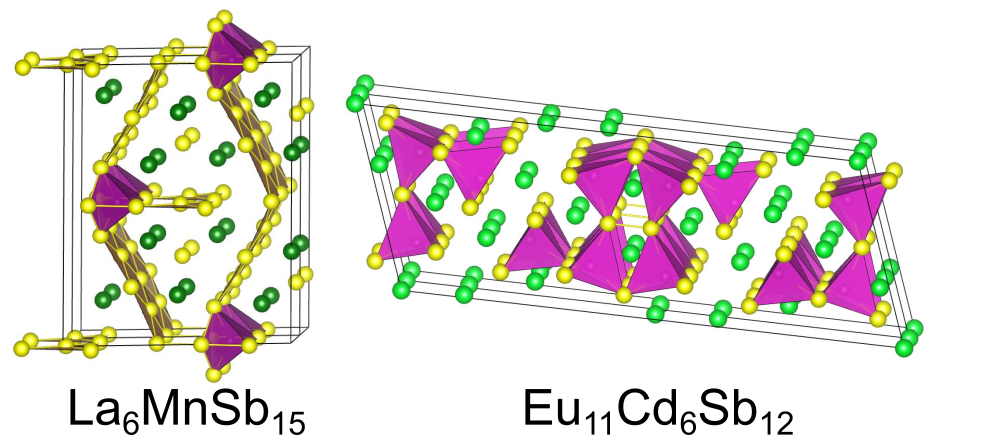
(3)Fill + Substitute
型構造の
サイトの3/4を
正方形で置き換えれば、充填スクッテルダイト型構造になります.残った
サイトも全て取り除くと通常のスクッテルダイト型構造となります.スクッテルダイトは熱電材料や超伝導体として有名です.
関連する構造として型構造があります.
まとめ
本記事では非常に多くの結晶構造が出てきましたが、報告されている膨大な数の結晶構造の中ではこれでもほんの一部です.とはいえ、これだけ多くの数の結晶構造が、非常に基本的な結晶構造から導けることがわかりました.見た目であまりに複雑な結晶構造だと考えるのをやめてしまいたくなりますが、落ち着いて部分部分を見ていけばどんな複雑な結晶構造であっても成り立ちが理解できます.
え、型構造?
型構造?頑張ればなんとかなるんじゃないでしょうか、うん.
参考文献
物性研究・電子版 Vol. 6, No. 1, 061206
U. Müller, Inorganic Structural Chemistry (Wiley, 2007).
結晶構造の描画にはVESTAを使用.K. Momma and F. Izumi, "VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data," J. Appl. Crystallogr., 44, 1272-1276 (2011).
*1:実際には、とても手に負えない結晶構造もあるにはありますが、できるだけ分かりやすく結晶構造を表現する方法を偉大な先人達が考えてくれています.