ポーリングの規則：結晶構造が成り立つためのルールとその現実

更新 2024-2-27

ポーリングの規則（Paulingの法則、ポーリング則、Pauling's principles）

ある元素の組み合わせと組成が与えられたときに、どのような結晶構造が安定であるかを予測することは可能でしょうか．

残念ながら現在でもこれは困難な課題であり、科学者の悲願となっています．近年では計算科学の進歩によってある程度の予測が可能になりましたが、複雑な組成・構造になると未だ手に負えません．

とはいえ、一見複雑に見える結晶構造であっても、一部分を見ると案外単純なユニットから構成されています．例えば、スピネル型構造は一見複雑ですが、四面体と八面体が点共有しているだけの単純な構造です．

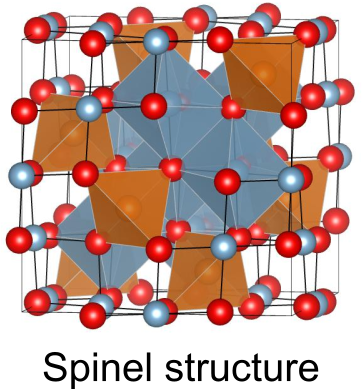
どのようなユニットが存在しうるかを明らかにできれば、どのような結晶構造が成り立つか予想することも不可能ではありません．そのためには、どのような結晶構造ユニットがあり得るか、あるいはあり得ないかについての知見を深める必要があります．

例として、イオン結合性の物質を考えましょう．

イオン結合性の物質では、各イオンの静電的相互作用によってある程度の局所構造が決まります．例えば、異符号のイオンはなるべく近くにいたいので、陽イオンは必ず陰イオンに囲まれ、陰イオンは陽イオンに囲まれます．同符号の陽イオン同士、陰イオン同士はお互いに反発し、なるべく遠ざかろうとします．

結晶を形成するために必要なルールはこれだけですが、実際の結晶構造は頭で考えるほど単純ではありません．配位数やイオンの分極率、電気陰性度などの情報も考慮すると、考えなければいけないことは山積みになります．

しかし、以上の単純な前提から驚くほど多くの情報を引き出すことが可能です．

イオン結合性の物質において、どのような結晶構造が実現するか、あるいは実現しないかを明示した５つの経験則が１００年近く前（１９２９年）に提唱されました．化学の巨人Linus Carl Paulingによって提唱された５つのルールを今日ではポーリングの規則と呼びます．

ポーリングの規則では、結晶構造中で陽イオン（陰イオン）がどのような局所構造にあるかを規定します．経験則ではありますが、結晶構造の予測・裏付けに有用であり、今日でも多くの固体科学者がポーリングの規則を念頭に置いて結晶構造を眺めています．

リンク

ポーリングの規則の概要

ポーリングの規則は、以下のような５つの法則から構成されます．

（１）ポーリングの第一法則：半径比に関する法則
「陽イオンの配位数は、陽イオンと陰イオンの半径比によって決まる」

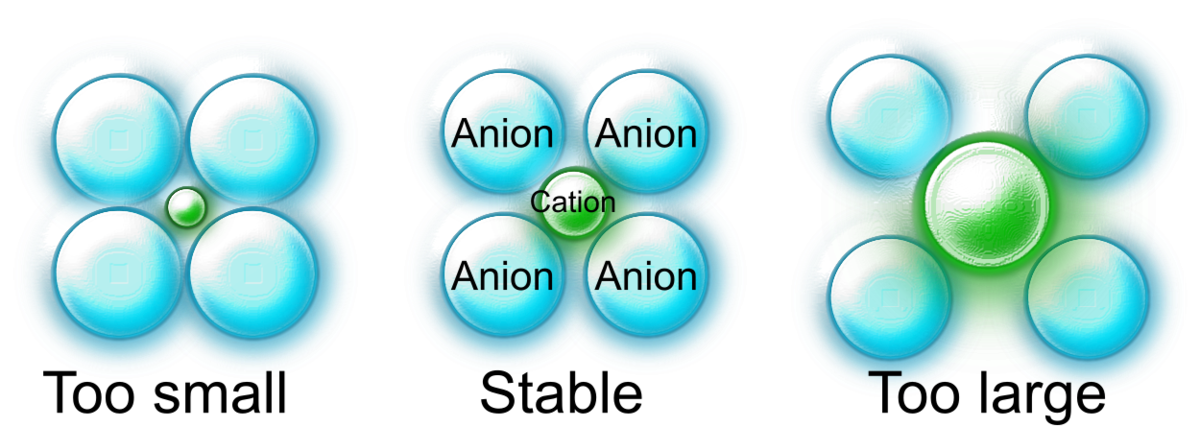
まず大前提として、ほとんどの陽イオンは陰イオンより小さく、陽イオンは大きな陰イオンに多面体型に配位されています．陽イオンと陰イオンの間の静電エネルギーを得するには、陽イオンに配位する陰イオンの数をできる限り多くすればよいです．

一方、陰イオンには当然有限の大きさがあるため、陽イオンに配位できる数には限りがあります．また、陰イオン同士は静電反発により互いをできる限り引き離そうとします．

これらの静電的な要請・幾何学的な要請を満たすために、陽イオンおよび陰イオンの大きさの違いによって異なる配位構造を作り出します．それゆえ、陽イオンと陰イオンのイオン半径の比をパラメータにすることによって、配位構造を予測することが可能になります．

ポーリングによれば、陽イオンと陰イオンが丁度接したときにもっとも配位構造が安定します．

大きい陽イオンであれば多くの陰イオンと接することができるため配位数が増え、小さい陽イオンでは配位数が減ります．ある配位構造をとった際に、陽イオンが陰イオンに接する条件は簡単な幾何学的な計算から求める事ができます．

第一法則は、物質によらず同じ配位数をとる元素（四面体配位を好むなど）では、よく成り立つことが知られています．一方、物質によって配位数が大きく変わるアルカリ金属や一部の遷移金属ではほとんど成り立ちません．[a]

（２）ポーリングの第二法則：静電原子価に関する法則
「安定な配位構造において，配位多面体の頂点をなす陰イオンの電荷は，多面体の中心にある陽イオンによる静電原子価強度によって相殺される」

さて、耳慣れない単語が出てきました．

「静電原子価強度」（electrostatic valence bond strength）は、陽イオンと陰イオンをつなぐイオン結合の静電原子価を、陽イオンの形式電荷を配位数で割った商であると定義します．

安定な結晶構造を持つには、周囲の全ての陽イオンから陰イオンに達する結合強度の和が陰イオンの電荷に等しくなっていなければなりません．

少しややこしいので具体例で考えましょう．

例えば、ペロブスカイトではは６つの酸化物イオンに、は１２の酸化物イオンに配位されています．

このとき、

（の静電原子価強度）＝（電荷数：）/ （配位数：）＝
 （の静電原子価強度）＝（電荷数：）/ （配位数：）＝

であり、一つの酸化物イオンは２つのと４つのに配位されているため、静電原子価強度の和は

 　　

となり、酸化物イオンの電荷（）に一致します．

かなり厳しい条件を与えている気がするルールですが、実際の物質ではどうでしょうか．

実際のところ、第二法則を満たす酸化物は全体の２０％程度しか存在しないようです．

一方で、第二法則から逸脱した値を示す物質は多面体が歪んでいるケースが多く、正多面体に近い配位構造を持つ物質に限れば、９０％程度が法則に適することが分かっています．[a]

（３）ポーリングの第三法則：多面体の連結に関する法則
「配位多面体における辺の共有、また特に面の共有は構造の安定性を低下させる」

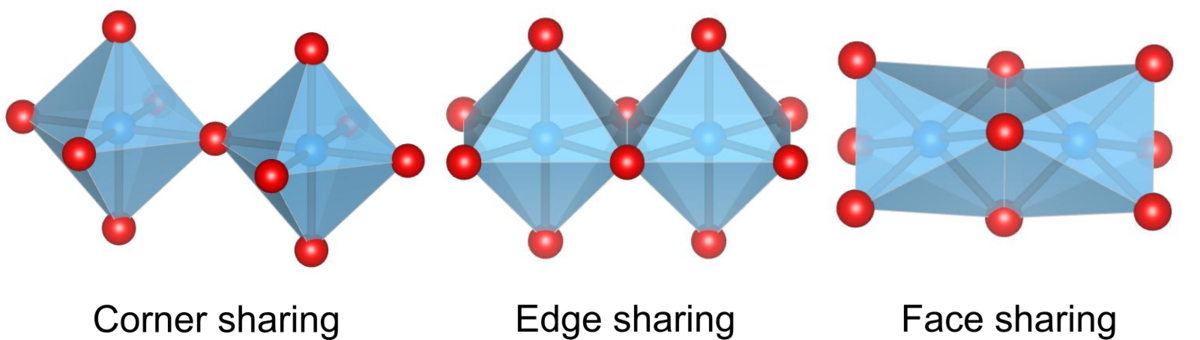
陰イオンに配位された陽イオンからなる配位多面体は、頂点、辺、面のいずれかを他の多面体と共有することによってネットワークを形成します．

例えば、ペロブスカイト構造では各八面体が頂点を共有しています．頂点共有 ＜ 辺共有 ＜ 面共有の順番で陽イオンー陽イオン間の距離が短くなるため、静電エネルギー的に不利となり、この順で構造が不安定化します．

第三法則に従えば、頂点共有＞辺共有＞面共有のように物質中に見つかる割合が多くなるはずです．

実際、全ての酸化物中の多面体の連結に関する調査では、頂点共有が６３％、辺共有が２７％、面共有が１０％であり、第三法則から予想される傾向と一致しています．

面共有が多い物質は陽イオンの配位数が多い物質が多く、配位数が８以下の物質に限った調査では、面共有は全体の２％しか現れませんでした．[a]

（４）ポーリングの第四法則：異なる種類の陽イオンに関する法則
「異なる種類の陽イオンを含む結晶では、高価数かつ少ない配位数をもつ陽イオンは、互いにまわりの多面体を共有しない傾向がある」

これは第三法則の補足であると言えます．

すなわち、高価数かつ少ない配位数をもつ陽イオンは、近くに他の陽イオンが存在する際の電子反発が大きくなるため孤立して存在することが多いと言い換えることができるかもしれません．

実際、配位数の少ない多面体は他の多面体と連結しない傾向があることが分かっています．一方で、高価数であるからといって必ずしも多面体の連結が少ないわけではないようです．

実際の構造を考える際には、静電作用だけでなく共有結合性や磁気相互作用の影響も重要であるため、ルールからの逸脱が見られます．

（５）ポーリングの第五法則：単純さに関する法則
「結晶中に含まれる本質的に異なる種類の成分の数は少ない傾向にある」

すなわち、結晶構造はいたずらに複雑になることはなく、可能な限り単純になるべきという法則です．

言い換えれば、ある陽イオンは一つの結晶構造中でたくさんの異なった配位構造になることはなく、可能な限り少ない配位構造を好む傾向を示します．

しかし、すぐマグネタイト（、鉄の四面体配位と八面体配位を含む）が例外として思い浮かぶように、あらゆる種類の物質に適応するルールではありません．

調査によると、おおよそ７０％の酸化物がこのルールに従うようです．

反対に、３０％の物質ではこの法則が成り立ちません．特にアルカリ金属やアルカリ金属では成り立たない物質が多いようです．[a]

リンク

まとめ

ポーリングの規則は、結晶化学が成立して間もない時期に、当時知られていた僅かな結晶構造とイオン結合への考察を組み合わせて見出された経験則です．結晶構造解析もほとんど普及していない時代にこのような一般則を導いたポーリングが、いかに驚異的であったかは論ずるまでもありません．

以上のようにポーリングの規則の主張は多岐にわたりますが、全ての法則を同時に満たすような結晶構造は全体の２割にしか満たないと指摘されています．[a]

「法則」と呼ぶには例外が多く、結晶構造を予測する上で過信することはできません．
しかし、それをポーリングの責任にすることはできません．ポーリングの法則が生まれてから１００年の間には、当然新しい結晶構造が生まれ例外も増えていきます．

むしろ１００年にわたってポーリングの法則に代わる法則が定着していないことの方が問題であって、物質科学の黎明期にこのような明快なルールを看破したのは見事としか言えません．

リンク

参考文献

[a] Angewandte Chemie, 2020, 132.19: 7639-7645.

セラミックス材料学（亀川厚則） 第３章 結晶構造

Pauling's rules - Wikipedia

結晶構造の描画にはVESTAを使用．K. Momma and F. Izumi, "VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data," J. Appl. Crystallogr., 44, 1272-1276 (2011).