更新 2024-3-2
ヒューム-ロザリーの法則(Hume-Rothery rules)
金属は、溶かして混ぜ合わせることにより固溶体(合金)を形成します.単体の金属では得られないような優れた特性を求めて、はるか古代より合金が利用され続けてきました.青銅や鋼はその顕著な例であり、単体の金属には見られない優れた強度や耐食性を示します.
鉄に少量のニッケルを加えた場合、ニッケルは結晶構造中で鉄が占めていたサイトを代わって占有します.この場合、原子レベルで均一に金属原子が混ざっており、このような固溶体を置換型固溶体と呼びます.一方、置換した原子が元の構造の隙間に入り込む場合もあり、侵入型固溶体と呼ばれます.
しかし、見た目で金属が混ざり合っていたとしても、原子レベルでは混ざり合っていないケースも存在します.鉄とニッケルは全組成範囲で固溶体を形成しますが、銅に鉄を加えても両者は決して混ざりません.
このように、金属元素の組み合わせによって「混ざり合うもの」と「混ざり合わないもの」が存在します.合金の合成は容易なので、どの金属とどの金属が混ざり合わないかというデータは蓄積されていきますが、それがなぜであるかは分かりませんでした.
20世紀前半、William Hume-Rotheryは過去の膨大な実験データを整理し、固溶体が形成するための要因を見出しました.この規則は今日、Hume-Rothery則と呼ばれます.
Hume-Rotheryの法則の成り立ち
Hume-Rotheryの法則は、いかにも2人の名前から来ているように見えますが、実際は一人の化学者William Hume-Rotheryに因む経験則です.この名は、同氏の祖父(Rothery)が、妻の旧姓(Hume)を併せてHume-Rotheryと名乗ったことに由来します.
Hume-Rotheryは青年時代に重病で聴覚を失いながらも、オックスフォード大学の教授職を勤め上げました.合金・金属間化合物に関する膨大な実験と経験則の発見で知られ、金属学の発展に重大な貢献を果たしています.
Hume-Rotheryが1934年に発表した論文で、固溶体が形成するために必要な要因として以下のものがあるとされました.
(1)原子の大きさ
元素AとBが置換型固溶体を形成するためには、金属が占めていたサイトを他の金属で置き換えなければなりません.元素Bが元素Aと同じ大きさの元素であればすんなりサイトに収まりますが、大きさの異なる元素であれば格子が歪まざるを得ません.ある程度以上の大きさの差があれば、サイトに収まりきらなくなります.
実験値によれば、原子半径に15%以上の差があると固溶体を形成しないことが明らかにされました.
侵入型固溶体の場合は大きさの制限が緩和され、60%の大きさの違いまで許容されるようになります.
 (2)電気陰性度
(2)電気陰性度
大きさが同程度であっても、必ずしも固溶体を形成するとは限りません.例えば、マグネシウムにシリコンを混ぜ合わせると、という金属間化合物が生成しますが、この結晶構造は
とは全く異なります.
これは、の電気陰性度(1.3)が
のもの(1.9)と大きく異なることが原因であり、固溶体の形成には電気陰性度が同じ程度の値であることが求められます.
(3)結晶構造
2つの元素が溶解するためには、結晶構造が同じである必要があります.各元素が常温でどのような結晶構造をとるかは直感的ではありませんが、おおむね周期表の属によって決まっています.
構造が異なれば周囲の配位環境も異なるため、原子が好みでない結晶構造をとればエネルギー的に不安定化し、固溶体を形成しない場合が多くなります.
(4)原子価
原子価(電子濃度)とは、ある元素の最外殻にあり化学結合や電気伝導に寄与する電子の数を指します.であれば1,
は2の原子価を持つとされます.他の要素が同じであれば、原子価の差の小さい元素が混ざり合いやすいです.
なお、原子価の小さい元素に原子価の大きい元素を固溶させる方が、その逆の場合より容易であるとされます.
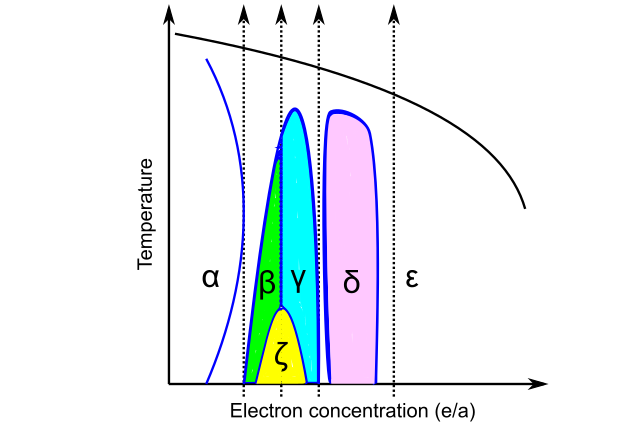
電子数と結晶構造
Hume-Rotheryは、金属の電子数と結晶構造の関係性についても重要な指摘をしています.ある合金において、価電子の総数と原子数の比()が一定であれば、元素や組成が異なっても同じ結晶構造の合金が得られるというものです.例を挙げましょう.
、
、
はいずれも体心立方格子の結晶構造を持ち、その他の特性もよく似ています.一見、何の関係性もなさそうな組成ですが、価電子の総数と原子数の比を計算してみましょう.
この通り、どれも同じの値(1.5)を示します.実際には、もう少し広い固溶範囲で同一の結晶構造をとりますが、この法則は他の多くの系でも見られます.
同様に、の
、
、
はγ-真黄銅型構造を、
の
、
、
は六方最密構造をとります.
固溶体や化合物の形成に原子価の概念を持ち込んで整理したこれらのルールをHume-Rotheryの法則と呼ぶ場合もあります.なお、はじめは経験則であったHume-Rothery則でしたが、後に理論的にも正当性が確認されています.
まとめ
合金は、有機化学のような工夫をしなくても合成が可能なため、理論の整備よりも前に莫大な実験データが蓄積されました.実際、金属がランダムに分布した合金材料の電子状態を計算することは現在においても容易ではありません.このため、合金の開発は勘と経験に頼ることが多かったのですが、Hume-Rotheryによって一定のルールが整備され、理論に基づいた材料開発の指針を与えました.
学会・産業界を問わずHume-Rotheryの考えが未だ根付いており、古くは準結晶の開発、現在ではハイエントロピー合金の開発にHume-Rothery則が活かされています.
参考文献
化学教育 1966 年 14 巻 4 号 p. 420-422
Materia Japan 2009 Volume 48 Issue 3 Pages 119-125
日本金属学会会報 1979 年 18 巻 12 号 p. 801-810
日本金属学会会報 1974 年 13 巻 10 号 p. 741-750
まてりあ 2006 年 45 巻 8 号 p. 605-610
The Hume-Rothery Rules for Solid Solution – Materials Science & Engineering