更新 2024-2-28
磁気格子と磁気フラストレーション
磁気の話ですので、磁性を持った原子について考えます.突然ですが、二次元に磁性イオンを敷き詰めることを考えてみましょう.どのような充填パターンが考えられるでしょうか.

まず、碁盤の目のように正方形の頂点上に磁性原子を配置したパターンが思い浮かびます.これを正方格子と呼びます.さて、磁性原子なので、原子の配置だけでなくスピンの向きについても考えてみましょう.
磁性イオン同士には磁気相互作用が働きます.強磁性的な相互作用の場合、スピンが同じ方向を向きたがります.この場合、スピンはすべて同じ方向を向けばいいので簡単です.
反強磁性体の場合ではどうでしょう.この場合、隣り合うスピンは反対方向を向きたがります.正方格子の場合、隣り合うスピンを逆向きに配置することは簡単です.下図のようにすれば完成です.

では、別の充填パターンについて考えます.図のように三角の頂点に磁性原子を配置してみましょう.このような格子を三角格子と呼びます.

さて、正方格子の時と同じように反強磁性的な相互作用を考えます.隣り合うスピンを反対向きにします.三番目のスピンを考えると、どちらを向かせればいいのか分かりません.

この場合、三角形の各頂点のすべての相互作用を満たすようなスピン構造が存在しないことが分かります.このような状況を磁気フラストレーション(幾何学的フラストレーション)と呼び、磁気構造が自明には定まりません.
物理学者は非自明なことに心惹かれる生き物ですから、磁気フラストレーションのある磁性体でどのような磁気物性が実現するか、昔から理論実験とともに研究が盛んにおこなわれてきました.
世の中には、正方格子や三角格子だけでなく、多種多様な格子が考案され、現実の物質で実現しています.それぞれに個性があり、格子ごとに愛好家がいます(多分).単純な磁気秩序だけではなく,時として量子スピン液体、スピンアイス、スピングラスなど時にエキゾチックな磁気物性の舞台となることが知られています.
本ページでは、三角格子やカゴメ格子など、様々な磁気格子についてまとめています.
- 磁気格子と磁気フラストレーション
- 様々な磁気格子
- 正方格子(Square Lattice)
- J1-J2 模型(J1-J2 model)
- Shastry-Sutherland 模型(Shastry-Sutherland model)
- CaV4O9 格子(CaV4O9 lattice)
- 三角格子(Triangle Lattice)
- メープルリーフ格子(Maple-leaf Lattice)
- カゴメ格子(Kagome Lattice)
- ハニカム格子(Honeycomb Lattice)
- スター格子(Star Lattice)
- オクタ‐カゴメ格子(Octa-kagome Lattice)
- スタゴメ格子(Stagome Lattice)
- ボウ‐タイ格子(Bow-tie Lattice)
- 正方晶タングステンブロンズ格子
- Fe5SiC格子
- まとめ
- 参考文献
様々な磁気格子
正方格子(Square Lattice)

まずはフラストレーションのない系から始めます.上述の通り、正方格子の磁気構造は自明に定まります.このため磁性体としてはあまり面白くないですが、それでも様々な物性の舞台となります.例えば、高温超伝導(同酸化物、鉄ニクタイド)は正方格子上の磁性原子が中心になって起こる劇的な現象です.
また、最近接の磁気相互作用(正方形の辺)を考えるだけではフラストレーションはありませんが、次近接相互作用(対角線ボンド)まで考慮に入れればフラストレーションが生じます.
正方格子を持つ代表的な物質
をはじめとした銅酸化物高温超伝導体
をはじめとした鉄系高温超伝導体
などのトポロジカル半金属
- 層状ペロブスカイト化合物
型構造,
構造
J1-J2 模型(J1-J2 model)

正方格子に対し、最近接の磁気相互作用(正方形の辺、)に加えて次近接相互作用(対角線ボンド、
)を考慮に入れたモデルです(あくまで格子としては正方格子のままです).
伝説の理論物理学者P. W. Andersonが正方格子におけるスピン液体状態と高温超伝導が密接に関連している可能性を提唱して以来、多くの理論的研究が行われました.
の極限、すなわち最近接相互作用が極端に大きい場合は、普通の正方格子と変わりません.反対に、
の極限では、対角線方向のスピンが反平行に並んだ磁気秩序が安定化します.
では,その中間では? 自明ではないですが、一般にスピン液体状態が現れると考えられています.
J1-J2 模型の代表的な物質 [1]
Shastry-Sutherland 模型(Shastry-Sutherland model)

なかなか厳つい名前が出てきましたが、単なる人名なので安心してください.
J1-J2 模型とは異なり、二本ある対角線の相互作用のうち一本だけを考慮に入れたのがShastry-Sutherland 模型です.提唱者であるB. S. ShastryとB. Sutherlandの名にちなんで名付けられました.
では、普通の正方格子と同じです.
の極限では、J1-J2 模型と同様に対角線方向のスピンが反平行に並び、二量体(ダイマー)を形成します.
しかし、そもそも対角線の一方のみを考慮したモデルなど非現実的で、机上の空論にしか見えないように思えますが....
驚くことに、実際の物質がShastry-Sutherland 模型と等価であることが発見されました.

この発見を機に研究が進展し、厳密なダイマー基底状態や磁化プラトー、非連続的な量子相転移,臨界点の存在など様々な興味深い物性が見つかっています.
Shastry-Sutherland模型の代表的な物質 [2]
CaV4O9 格子(CaV4O9 lattice)

その名の通り、で見られる格子です.正方格子から原子を1/5取り去ることで形成されます.スピンギャップなどの性質が知られています.
自体は最近、電池材料としても注目されています.[3]
三角格子(Triangle Lattice)

上述の通り,最も単純なフラストレーション格子です.球を隙間なく平面に敷き詰めたときに現れる格子であり、最も自然に表れやすい配置であると言えます.実際、多くの物質中において三角格子が見られます.
低温まで冷却すると格子が歪んでフラストレーションを解消する物質がある一方で,最低温まで三角格子を維持する物質も存在します.磁気異方性(スピンが特定の方向を向きやすい性質)の強さにもよりますが、互いに120°をなす三角構造が見られる場合があります.
このように、相互作用の競合によって、全ての相互作用エネルギーを最低にすることはできませんが、互いに120°をなして配置することで一部妥協した状態が実現します.磁気異方性が強いと、フェリ磁性相や部分無秩序構造が見られます.
スピンが120°構造をなした際に、正三角形の頂点を右回りに順にスピンの向きを見た場合に、スピンが「右回り」になる場合と「左回り」になる場合があります.この違いをスピンカイラリティと呼び、巨大な異常ホール効果などの物性の起源となっています.
三角格子を持つ代表的な物質 [4]
メープルリーフ格子(Maple-leaf Lattice)

三角格子から派生する格子です.その名の通り、メープル(カエデ)の葉に似ていることから名づけられました.
三角格子から7分の1の原子を取り去ることによって形成されます.三角格子では最近接の原子の数が6でしたが、メープルリーフ格子では5になります.
メープルリーフ格子の実験的な研究は多くないですが、互いに120°をなす三角構造か3つのスピンが三量体(トリマー)を示す基底状態が予測されています.
メープルリーフ格子を持つ代表的な物質 [5]
- Spangolite
カゴメ格子(Kagome Lattice)

やけに日本語的な響きがしますが、実際、日本語の「籠の目」が名前の由来です.Kôdi Husimi氏によって1951年に名づけられています.
三角格子から4分の1の原子を取り去ることによって形成されます.
最近接の原子の数が三角格子では6、メープルリーフ格子では5でしたが、カゴメ格子では4となります.最もフラストレートした格子とも呼ばれます.
そのため、量子スピン液体の候補材料として数々の物質が研究されてきました.カゴメ磁性体はなぜか天然鉱物に多く見られ,(ハーバートスミス石),
(ベシニエ石),
(ボルボサイト)などが知られています.
一方で近年になって、カゴメ格子がトポロジカル的に保護されたバンド状態や分散のないフラットバンドの舞台になることが予測され、爆発的に研究が進行しています.
例を挙げると,
や
における巨大なホール効果, Weyl 半金属状態
や
におけるDiracバンドおよびフラットバンド
における電荷秩序や超伝導
これらの研究の熱はまだまだ冷めそうにありません.
カゴメ格子を持つ代表的な物質 [6]
(ハーバートスミス石)
ハニカム格子(Honeycomb Lattice)

ハチの巣格子としておなじみのハニカム格子です.強度に優れることでも知られ、建造物や航空機でもこの構造が用いられています.また、グラフェンやグラファイトの構造としても有名です.
ハニカム格子は、三角格子から半分の原子を取り去ることによって形成されます.
最近接の原子の数が三角格子では6、メープルリーフ格子では5、カゴメ格子では4でしたが、ハニカム格子では3となります.
これらの類似構造とは異なり、最近接相互作用のみを考える限りではハニカム格子にはフラストレーションがありません.しかし、最近接と次近接の距離が近いので、結局のところフラストレーションのある系が多いです.
Kitaev 模型と呼ばれる条件を満たすハニカム格子では、量子スピン液体状態が実現することが知られています.また、電池材料としても多くの物質が知られています.
ハニカム格子を持つ代表的な物質 [7]
- グラフェン,グラファイト
型構造
スター格子(Star Lattice)

カゴメ格子からの派生です.
カゴメ格子は六角形と三角形の組み合わせでしたが、スター格子ではなんと十二角形と三角形の組み合わせから成ります.
スター格子を持つ代表的な物質 [8]
オクタ‐カゴメ格子(Octa-kagome Lattice)

こちらもカゴメ格子からの派生です.八角形と三角形の組み合わせから形成されます. [9]
スタゴメ格子(Stagome Lattice)
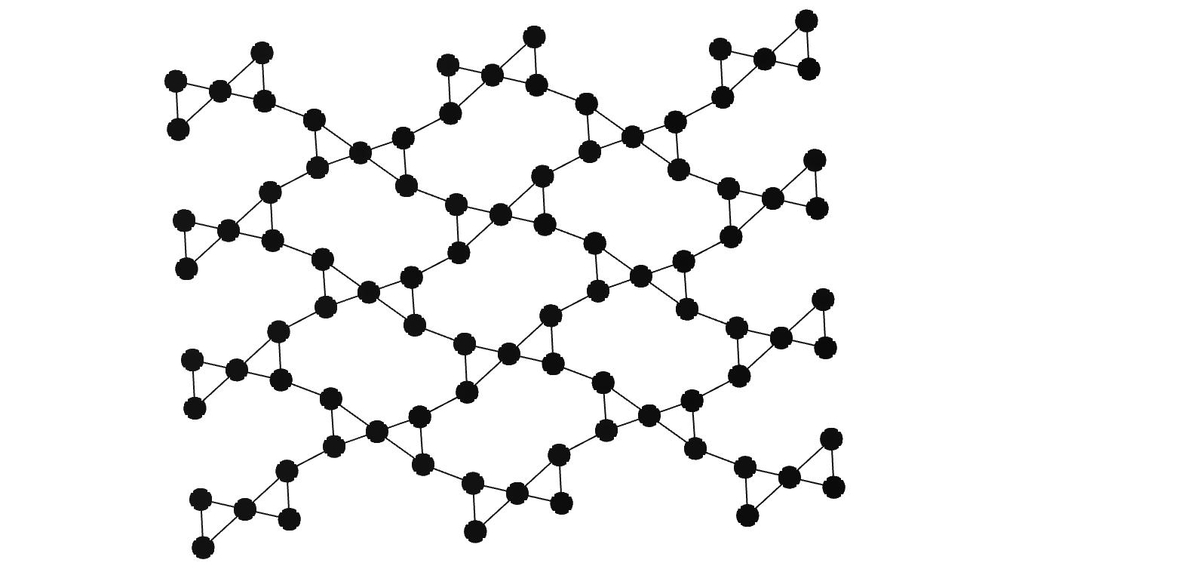
またしてもカゴメ格子からの派生です.今度は十角形と三角形の組み合わせです. [10]
ボウ‐タイ格子(Bow-tie Lattice)

カゴメ格子の変種と言うべきでしょうか.三角形と六角形から構成されています.
カゴメ格子と同じように強いフラストレーションが期待できそうですが、モデル物質は多くありません.
ボウ‐タイ格子を持つ代表的な物質 [11]
-
正方晶タングステンブロンズ格子

正式名称であるかは知りません.正方晶タングステンブロンズ(TTB)を上から見た時に現れる格子です.三角形と五角形と六角形が見えます. [12]
Fe5SiC格子

正式名称はたぶんないです.筆者が物質探索をしていた際に偶然見かけました.
三角形と五角形を組み合わせた珍しい格子です. [ag]
まとめ
探してみると様々な磁気格子があることが分かりました.理論的にはどれもよく研究されているのですが、実験するにはモデル物質がなければ始まりません.
むしろ、自然はよくもこれほど多様な格子を現実にもたらしてくれたものだなあと思います.
また、格子の形だけでなく、相互作用の強さも重要なパラメータです.まだまだ理論的にも解明できない現象がフラストレーション系には潜んでいるそうなので、新しいモデル物質がたくさん出てきてほしいところです.
参考文献
[1] Journal of the Physical Society of Japan, 2005, 74.6: 1702-1705. / Physical Review B, 2001, 64.2: 024409. / Physical Review B, 2017, 95.6: 064408. / Physical Review B, 2018, 98.5: 054422.
[2] Physical review letters, 1999, 82.15: 3168. / Progress of Theoretical Physics Supplement, 2002, 145: 17-22. / Physical Review B, 2008, 77.3: 035135.
[3] Journal of the Physical Society of Japan, 1997, 66.3: 793-802.
[4] Journal of the Physical Society of Japan, 1978, 44.3: 806-812. / Science, 2005, 309.5741: 1697-1700. / Nature materials, 2020, 19.10: 1062-1067. / Journal of the Physical Society of Japan, 1985, 54.9: 3526-3536. / Journal of the Physical Society of Japan, 1997, 66.6: 1607-1610.
[5] Journal of Physics: Condensed Matter, 2011, 23.16: 164201. / Physical Review B, 2018, 98.6: 064412.
[6] Journal of the Physical Society of Japan, 2010, 79.1: 011001. / Nature, 2015, 527.7577: 212-215. / Nature communications, 2018, 9.1: 1-8. / Physical Review Materials, 2019, 3.9: 094407. / Nature, 2020, 583.7817: 533-536. / Nature materials, 2020, 19.2: 163-169.
[7] Science, 2017, 356.6342: 1055-1059. / Materials Research Bulletin, 2014, 50: 292-296. / Physical review letters, 2015, 114.7: 077202.
[8] Journal of the American Chemical Society, 2020, 142.11: 5013-5016. / Angewandte Chemie International Edition, 2007, 46.32: 6076-6080.
[9] Journal of the American Chemical Society, 2017, 139.40: 14057-14060.
[10] Chemistry of Materials, 2021, 33.6: 2173-2177.
[11] Journal of Materials Chemistry C, 2018, 6.16: 4541-4548. / Materials Advances, 2021, 2.24: 7939-7948. / Dalton Transactions, 2013, 42.41: 14718-14725.
[12] Angewandte Chemie, 2017, 129.21: 5864-5867.
[13] Journal of alloys and compounds, 2006, 407.1-2: 98-105.
結晶構造の描画にはVESTAを使用.K. Momma and F. Izumi, "VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data," J. Appl. Crystallogr., 44, 1272-1276 (2011).