更新 2024-3-3
遮蔽効果(Shielding effect)
全ての物質は原子から構成されており、原子の中には正の電荷を持つ原子核と負の電荷を持つ電子があります.電子は原子核の周りを飛び回っており、K殻、L殻…と呼ばれる電子殻に決まった数だけの電子が収容されています.おおむねこのような認識で問題ありませんが、実際にはもう少し複雑なことが起こっています.

原子核と電子は異符号であるので互いを引き付け、それゆえ電子は原子から離れることなく束縛されます.原子番号1番の水素であれば、電子も原子核も一つしかないので、一つの電子が原子核のクーロン力を全て引き受けます.
一方、原子番号3番のリチウムでは、電子が3つありますが、各々の電子が原子核から感じるクーロン力は平等ではありません.より外側にある電子では、原子核からのクーロン力が他の電子によって弱められるのです.
このように、ある電子に働く原子核からのクーロン力が他の電子の存在によって弱められている状態を、遮蔽効果が働いていると表現します.遮蔽効果は、電子が複数あることによって起こる現象で、原子や分子の基礎物性や反応性の違いを非常にうまく説明することが可能です.
今回は、遮蔽効果について詳しく見ていきます.
電子が増えると起こること
核電荷の遮蔽
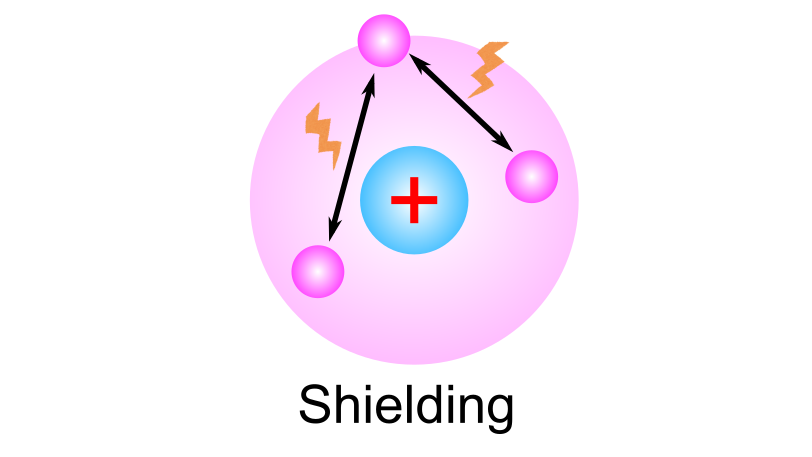
正の電荷を持つ原子核が一つと負の電荷を持つ電子が一つあるとします.核の電荷がであるとすれば、ひとつの電子は核の全電荷を全て感じ、全電荷数に比例したクーロン力が働きます.
原子核と電子の間に別の電子
が一つあるとすればどうでしょうか.2つの電子の間には反発力が働きます.
それゆえ、電子には原子核から引き寄せられる電子
と反発する力が働き、原子核が電子
を引き付けるクーロン力は相対的に弱められます.これが遮蔽です.電子が複数存在することによって、核から働くクーロン力が実効的に弱まったように見える現象です.遮蔽によって弱まった核電荷を実効核電荷と呼びます.
遮蔽定数
電子殻には内側から順にK殻、L殻、M殻…とあります.外側にある電子ほど、内側にある電子による遮蔽を大きく受け、実効核電荷が小さくなります.実効核電荷が小さいということは、電子を束縛する力が弱いということです.これにより、周期表の下に行けば行くほどイオン化エネルギーが小さくなる理由を説明することが可能です.
遮蔽効果の大きさを量子力学的に計算することは非常に複雑で難しいことです.それゆえ、近似的に各電子に働く有効核電荷を推定することが行われています.
この有効核電荷の減少分を遮蔽定数と呼びます.
が大きくなるほど遮蔽効果が大きいと言え、一般に
が大きいほど遮蔽効果は大きくなります.
の水素でのみ
となります.
有効核電荷と原子番号
以下で、有効核電荷が原子番号とともにどのように変化するかを見ていきましょう.
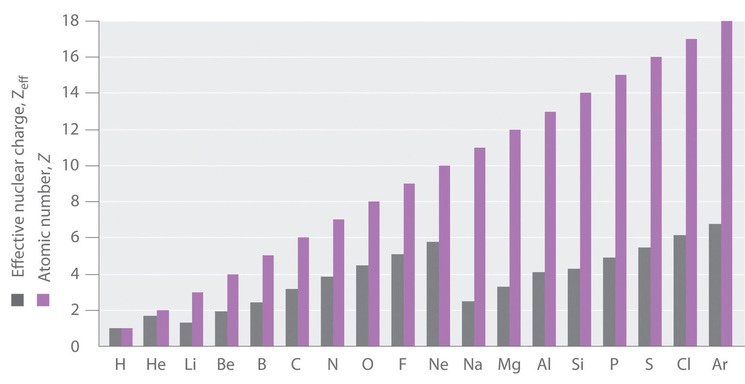
核電荷(原子番号)の増大とともにが順調に大きくなるように見えますが、ところどころで
が減少する箇所もあることが分かります.
これは元素の属する周期が変わった箇所であり、電子殻が切り替わったことで内殻の電子数が一気に増え、も小さくなります.
電子の軌道と遮蔽効果
遮蔽効果は電子殻によってのみ決まるものではありません.同じ電子殻(K殻、L殻、M殻…)にある電子でも、角運動量の違いによってs軌道、p軌道、d軌道、f軌道…と異なる軌道に属します.
これらはそれぞれ方位量子数と呼ばれるパラメータが異なり、電子が存在する軌道の形が大きく異なります.詳しくは物理化学や量子力学の教科書を参照してもらうこととして、話を進めます.
原子に存在する電子が一つだけであれば、s軌道、p軌道、d軌道、f軌道…のいずれに属しても平均のエネルギーは変わりません.しかし、電子が複数あると話は変わり、軌道によってエネルギーが異なってきます.これは、軌道の形状がそれぞれ異なるためです.
s軌道は球対称であり、概して原子の中心で最も電子の存在確率が高く、離れていくに従って存在確率が下がります.p軌道、d軌道、f軌道と進むごとに、電子の存在確率がゼロとなる領域(節)が原子の中心付近で増え、原子から離れた位置に電子が存在する確率が高くなっていきます.すなわち、s軌道の電子は他の軌道の電子の内側に「潜り込む」ことが多くなります.これを貫入と呼びます.
貫入が起これば、その分遮蔽する力が強くなり、効果的に有効核電荷を弱めます.最も核に近い1s電子は最も強い遮蔽効果を示します.2p軌道の電子から見れば、核の近くに近寄ることがないため、1s電子の遮蔽をより強く受けます.一方で、2s軌道には核電荷の近くまで侵入する電子が存在するため、遮蔽効果の一部を回避する(遮蔽が弱まる)ことができます.
s > p > d ~ f
1s > 2s > 2p > 3s > 3p > 4s > 3d > 4p > 5s > 4d > 5p > 6s > 4f
f軌道は特に遮蔽効果が小さく、ランタノイド収縮の原因となります.
スレーターの規則
有効核電荷を理論的に求めるのは困難ですが、経験的にどのような値をとるかが知られています.最も有名な経験則は1930年にJohn Slaterによって提唱された以下のようなルールであり、スレーターの規則として知られています.
まとめ
水素には電子が一つしか存在しないため、状況を比較的シンプルに記述することができます.しかし、電子の複数ある多電子原子では状況は一気に複雑になります.そこで、電子が受ける正電荷を別の電子が減少させるという遮蔽効果の概念により、水素のような軌道と有効核電荷(Zeff )を使って、複雑な原子やイオンの電子分布を簡略化して表現することができます.
厳密な計算というよりは経験的な値ですが、現実の事象(例えばイオン化エネルギーの変化)を驚くほど的確に言い当てることが可能です.
参考文献
7.2: Shielding and Effective Nuclear Charge - Chemistry LibreTexts
シュライバー・アトキンス無機化学(上)第4版