磁化率の測定データをどのように解析・解釈すればよいか

更新 2024-3-5

磁化率（Magnetic susceptibility）

磁気物性は、物質の最も基本的な性質の一つです．新物質・未知物質が得られたとき、一番最初に行われる測定が磁気物性の測定であることも珍しくありません．

磁気物性の測定装置は様々な研究所にあり、共同利用も含めればあらゆる研究者が利用できます．測定の自動化も進み、初学者であっても測定自体は手軽にできるようになりました．

しかし、実験をしてデータを得ても、そこからが大変です．得られたデータを解析し、人間に理解できる形に翻訳しなければなりません．磁性学は非常に難解で、教科書を読んで理解したとしても、実際に測定データを解析・解釈するのは簡単なことではありません．

例えば、磁気測定から得られる非常に重要なパラメータとして磁化率（帯磁率）があります．

　　 $M = χH$
( $M$ :磁化、 $χ$ : 磁化率、 $H$ :磁場)

これは外部磁場によって物質がどのくらい磁化されやすいかを示した値です．磁化率の温度依存性から、物質がどのような磁気的性質を示すかが分かります．

磁化率の温度依存性は様々ですが、それぞれをどのように見分ければよいでしょうか．

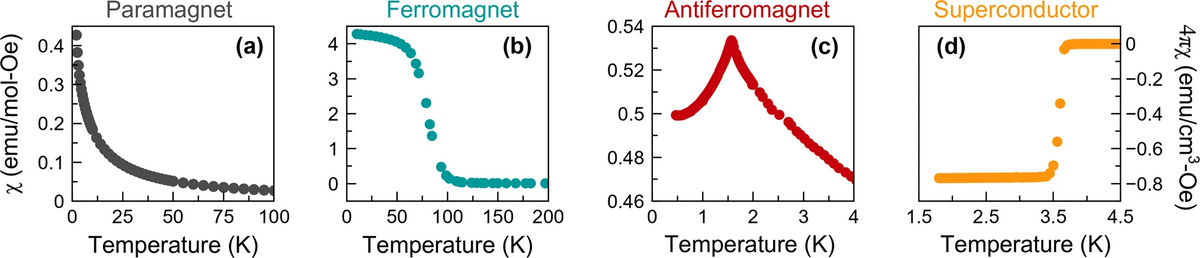
Examples of ordering transitions in magnetic susceptibility.
(This article is licensed under a Creative Commons Attribution 4.0 International License)

磁化率（Magnetic susceptibility）
磁化率の起源
磁化測定の実際
まとめ
参考文献

今回は、Commmunication Physics誌に出版されたチュートリアル記事を参考に、磁化率測定から得られたデータの解析法と、そこから得られる解釈について解説します．

"Tutorial: a beginner’s guide to interpreting magnetic susceptibility data with the Curie-Weiss law." Communications Physics 5.1 (2022): 95.

This article is licensed under a Creative Commons Attribution 4.0 International License

（参考）

磁性学の単位系にはCGS系とSI系が未だ混在しており、装置や分野によって使い分けられています．両者は互いに変換可能であり、例えばモル透磁率には以下のような関係があります．

　　 $m^3 \text{/} mol (SI) = 4π×10^{-6} \rm{emu \text{/} mol (CGS) }$

なお、CGS単位系では $\rm{emu×Oe^{-1}}$ は $\rm{emu}$ と同じことを意味するので、しばしば $\rm{Oe}$ は省略されます．

リンク

磁化率の起源

物質に磁場を印加すると磁化されます．どれだけ磁化されやすいかを示した値が磁化率です．磁化率に寄与する要因は様々であり、物質によってその割合が大きく異なります．詳細は磁性学の教科書を参照してもらうこととして、以下では概略を述べます．

軌道反磁性

電子の軌道運動によってもたらされる成分で、反磁性磁化率（ $χ_D$ ）は次式で与えられます．

　　 $χ_D = -\dfrac{ne^2}{6m_ec^2}[r^2$ ] (CGS)
　　 $χ_D = -\dfrac{nμ_0e^2}{6m_e}[r^2$ ] (SI)
( $n$ : 電子数、 $μ_0$ : 真空の透磁率、 $e$ : 電荷素量、 $[r^2$ ]: 電子軌道の平均二乗半径、 $m_e$ : 電子の質量、 $c$ : 光速、負の符号は反発を意味する)

負の値を持ち、温度に依存しません．値は小さいため、多くの磁性体では無視できます．考慮する場合は、下記文献から各構成イオンにおける値を探して全原子の合計をとることで求められます．

Bain, G. A. & Berry, J. F. Diamagnetic corrections and Pascal’s constants. J. Chem. Educ. 85, 532 (2008).

Curie-Weiss常磁性

全ての物質で生じる反磁性とは異なり、常磁性は不対電子をもつ「磁性体」でのみ見られます．磁気相互作用に比べて高温では、磁性イオン同士は熱揺らぎによって無秩序に振る舞います（低温では、温度よりも磁場による影響がより優勢になります）．

Curie-Weiss則は、常磁性状態を記述した関係式です．

　　 $χ=\dfrac{C}{T-θ_{CW}}$ (CGS, SI)
( $C$ : キュリー定数、 $θ_{CW}$ : Curie-Weiss温度)

Curie定数 $C$ は不対電子数と相関があり、有効磁気モーメント $μ_{eff}$ とは以下の関係があります．

　　 $μ_{eff} = \sqrt{8C} μ_B$ (CGS)
　　 $μ_{eff} = 800\sqrt{C} μ_B$ (SI)

なお、有効磁気モーメントは下式から計算された磁気モーメント $μ_{cal}$ の値と比較検討することができます。

　　 $μ_{cal} = g_J\sqrt{J(J+1)}μ_B$

キュリー・ワイス温度 $θ_{CW}$ は、物質内の磁性イオン同士の相互作用の程度を表します．

正の $θ_{CW}$ は磁性イオン同士に強磁性的な相互作用が働いていることを示し、負の $θ_{CW}$ では反強磁性的な相互作用があることを示します．

$θ_{CW}$ の絶対値に近い温度になると磁気相互作用が増して常磁性ではなくなり、それ以下の温度ではキュリー・ワイスの仮定が成り立たなくなります．

強磁性体では、転移温度 $T_C$ とキュリー・ワイス温度 $θ_{CW}$ がほぼ等しくなりますが、反強磁性体では $θ_{CW}$ の方が高くなるケースが一般的です．Curie-Weiss則は絶縁体、かつ４ｆ電子か３ｄ電子を持つ物質でよく成り立ちます．

van Vleck常磁性

以上の常磁性では、磁場が角運動量の基底状態に与える影響のみを考慮しています．しかし、より高エネルギーの角運動量状態を考慮することによって、励起状態に依存した新しい常磁性の項が得られます．このvan Vleck常磁性項は正の値で、かつ温度に依存しない値を持ちます．

van Vleck常磁性項は角運動量状態間のエネルギーギャップが小さいほど大きくなり、大抵の物質では無視できるほど小さな値ですが、 $\rm{Eu^{3+}}$ と $\rm{Sm^{3+}}$ を含む物質では無視できない値を持ちます．

パウリ常磁性とランダウ反磁性

絶縁体では磁気イオンは孤立していますが、金属では伝導電子が磁性を担います．伝導電子による常磁性はパウリ常磁性と呼ばれ、温度に依存しない正の値を示します．これは、磁場をかけることで伝導バンド内のアップスピン電子とダウンスピン電子のバランスが崩れ、差し引きの磁化が現れることに起因します．

　　 $χ_p = μ_B^2g(E_F)$ (CGS)
　　 $χ_p = μ_0μ_Bg(E_F)$ (SI)

パウリ常磁性は通常小さな値を示し、 $\rm{10^{-4}-10^{-5} emu/ mol}$ 程度です．

伝導電子による反磁性の寄与もあり、ランダウ反磁性と呼ばれます．自由電子モデルではランダウ反磁性はパウリ常磁性の３分の１の値ですが、負の値を持ちます．この比は物質のバンド構造や有効質量の値によってばらつきがあるようです．

伝導電子による温度に依存した磁化率

伝導電子による常磁性成分は通常小さな値ですが、電子間に強い相関がある場合は比較的大きな寄与が見られます（遍歴磁性体）．遍歴磁性体でも、高温ではキュリーワイス的な常磁性磁化率が見られます．すなわち、絶縁体であっても金属であっても磁性体は高温では同じくキュリーワイス的な振る舞いをします．

しかし、遍歴磁性体では根本的な物理が異なるため、得られたキュリー定数などの値が有効モーメントと直接的には結びつかないという点に注意が必要です．一般に、得られるキュリー定数の値は非常に小さな値となります．

磁化率の起源のまとめ

以上をまとめると、十分に高温では磁性体の磁化率には以下のような成分が含まれます．

・Curie-Weiss常磁性

・温度に依存しない常磁性（van Vleck常磁性、Pauli常磁性（金属））

・温度に依存しない反磁性（軌道反磁性、ランダウ反磁性（金属））

温度に依存しない成分は通常小さいため、Curie-Weiss常磁性がほとんどの振る舞いを決定します．

温度をキュリー・ワイス温度 $θ_{CW}$ 以下に下げると、磁気秩序やスピン凍結の影響によってキュリー・ワイス則からのずれが見られます．ずれが顕著になり、磁化率が極大値をとったり急激に上昇し始める温度が転移温度です．

典型的には下図のように振る舞います．

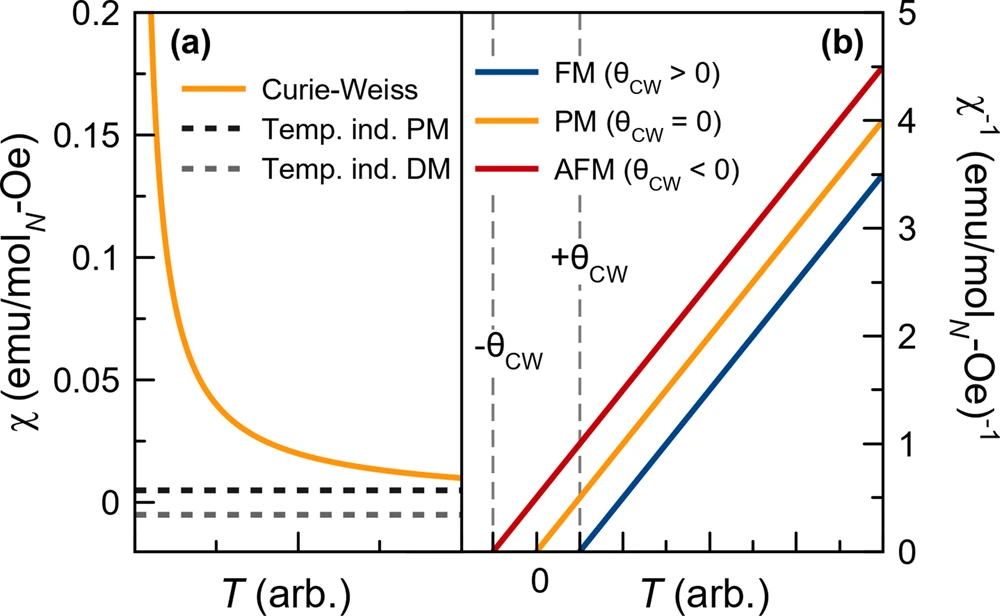
Appearance of Curie–Weiss behavior in direct and inverse susceptibility.　
(This article is licensed under a Creative Commons Attribution 4.0 International License)

磁化率測定から転移温度を読み取ることは可能ですが、磁気秩序の様子については定性的にしか分かりません．中性子回折測定やNMRの実験によって詳細な分析をする必要があります．

さて、ここまで磁化率にどのような成分が含まれているかを見てきました．以下では、実際に試料の磁化率を測定した後にどのような手順を踏んで解析をするのか見ていきます．なお、磁場は直流、試料は粉末のものを使用することとします．

リンク

磁化測定の実際

１．事前準備

測定前に、試料の重量を正確に測定し記録します．できれば精密天秤を使用し、三回測定をして平均を求めます．

２．測定設定

測定パラメータを設定します．ここでは、バックグラウンドの影響を最小限に抑える方法でサンプルを設置（多結晶体サンプルには、倒立ゲルカプセルを推奨）し、適切な試料量と印加磁場の大きさを選択します．

測定方法については、装置のユーザーマニュアルを参照してください．試料の質量および印加磁場を増加させれば全体的なS/Nが向上する効果があります．一方で、 $M$ と $H$ の間の線形関係は高磁場では崩れる可能性があることに注意してください．

３．測定および生データの取り出し

装置のマニュアルを参考に、測定を行い、データを取り出します。

４．データの変換

　得られた磁化の値を下式からモル磁化率（ $χ_{mol}$ ）に変換します．

　　 $χ_{mol} = \dfrac{M (emu)}{H (Oe)} \dfrac{M (g\text{ }mol^{-1})}{m (g) n}$
( $M$ [emu]: 磁化、 $M$ [g / mol]: モル質量、 $H$ : 印加磁場、 $m$ : サンプル質量、 $n$ : 単位式あたりの磁気イオンの数)

nが未知の場合はn = 1として単位式あたりのモル磁化率を求めます．

５．磁化率のプロット

$χ_{mol}$ vs 温度 $T$ のプロットを作成します．試料には、前節で挙げた要因のうちどの磁化率の寄与が含まれるかを考えます．キュリーワイス(局所モーメント)の寄与があると考えられる系であれば、磁気転移温度以上の温度で磁化率が単調減少する振る舞いが見られるはずです．

６．磁化率の逆数のプロット

$χ_{mol}^{-1}$ vs 温度 $T$ のプロットを作成します．直線的な振る舞いをする領域があれば、その範囲でキュリー・ワイスの式に従ってフィッティングを行います．

　　 $χ^{-1} = \dfrac{T-θ_{CW}}{C} = \dfrac{T}{C} - \dfrac{θ_{CW}}{C}$

これにより、傾きが $\dfrac{1}{C}$ 、切片が $θ_{CW}$ に相当する直線が得られるはずです．これとキュリー定数の式から、有効磁気モーメントが求められ、理論的に予測される値と比較できます．

７．フィッティングの際の注意

全てのフィッティングは $χ_{mol}$ vs $T$ ではなく $χ_{mol}^{-1}$ vs $T$ の図に対して行うべきです．前者では、フィッティングの重みが（キュリー・ワイス的な振る舞いから外れた）低温領域に置かれてしまうためです．

また、磁化率の温度に依存しない項は前者では視覚的に見えにくいことも理由の一つです．

なお、 $χ_{mol}^{-1}$ vs $T$ でのフィッティングの範囲は磁気転移温度よりも高温側になるように注意深く選定します．温度範囲を変えても同じような値が得られるかも確認します．

８．定数項の扱い

もし、 $χ_{mol}^{-1}$ vs Tのプロットが直線的な振る舞いから外れていた場合、温度に依存しない定数項 $χ_0$ が悪さをしているかもしれません．

Effect of a temperature independent contribution to susceptibility on Curie–Weiss behavior.
(This article is licensed under a Creative Commons Attribution 4.0 International License)

$χ_0$ の値が比較的小さくても、 $χ_{mol}^{-1}$ としてプロットすれば寄与が大きく見えます．この定数項には軌道反磁性やパウリ常磁性など様々な起源が考えられます．

この場合、キュリーワイス則に定数項を加えて修正した式を用いてフィッティングを行います．

　　 $χ = \dfrac{C}{T-θ_{CW}} + χ_0$
　　 $χ^{-1} = \dfrac{T-θ_{CW}}{χ_0(T-θ_{CW}) + C}$

各常磁性・反磁性の大きさは理論的に予想が可能なため、得られたχ0の値が期待される値から大きく逸脱していないかも合わせて確認します．

まとめ

以上の手順に沿えば、多くの場合でキュリーワイスフィッティングがうまくいきます．しかし、物質系によってはまた別の寄与を考えなくてはならない場合もあります．局所磁気モーメントが存在する場合でも、低次元性、高スピンから低スピンへのクロスオーバー、中間価数など、キュリーワイスの挙動を破綻させる要因は他にもあります．これらはそれぞれ帯磁率に特徴的な温度依存性をもたらし、従来のキュリーワイスの振る舞いから逸脱させます．

では、どのようにすればよいか．キュリーワイスの法則を適用する際に考慮しなければならない特別なケースについては、元の論文で詳しく述べられています．

参考文献

Mugiraneza, Sam, and Alannah M. Hallas. "Tutorial: a beginner’s guide to interpreting magnetic susceptibility data with the Curie-Weiss law." Communications Physics 5.1 (2022): 1-12.

はじめよう固体の科学

電池、磁石、半導体など固体にまつわる話をします