更新 2024-2-25
仕事関数(Work function)
物質中には途方もない数の電子が存在しており、それぞれ異なるエネルギーを持ちます.電子は任意のエネルギーを自由に取ることができず、量子力学的な制約により、エネルギー準位によって指定される決まったエネルギーだけを占めます.
既に電子が占めている準位を新たに占有することはできないため、電子はエネルギーの低い準位から順々に詰まっていくことになります.最後に入る電子は当然最も高いエネルギーを持っており、それゆえ最も高い反応性を示します.
物質に(光や電気によって)エネルギーを与えたとき、電子が原子核の束縛から逃れて物質外部に飛び出してくる場合があります.ガス中にある孤立した原子から電子を一つ物質の外部へ叩き出すために必要なエネルギーをイオン化エネルギー(IE)と呼びます.
これは高等学校の化学でも習う、物質の基礎パラメータの一つです.
ここで、はガス状の原子または分子であり、
は電子が一つ取り去られた後の一価カチオン、
は取り去られた電子です.
一方、今回の主役となる仕事関数は「バルク材料(固体または液体)」の電子を一つ取り除くのに必要なエネルギー量」を意味します.
仕事関数の大小によって物質の反応性や安定性を評価することが可能になります.仕事関数の記号としてが使用されます.
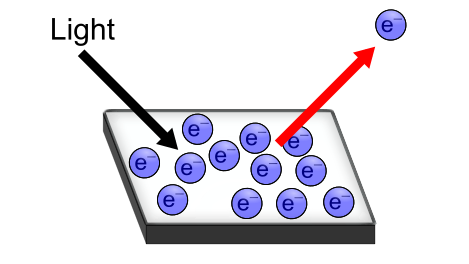
仕事関数の概要
仕事関数は、より正確には「電子をフェルミ準位から真空に取り出すのに必要なエネルギー」と定義されます.
フェルミ準位とは、電子が占有しているエネルギー準位と電子が空のエネルギー準位の境界の準位を意味します.金属はバンドギャップがなく、バンド内にフェルミ準位があります.
一方、半導体・絶縁体におけるフェルミ準位はバンドギャップ内に位置しており、その占有確率がちょうど50%になるエネルギーの点を指します.すなわち、通常の(添加のない)半導体では価電子バンド上端と伝導バンド下端のちょうど真ん中の位置とされます.
固体のイオン化エネルギーは仕事関数とよく似ていますが、少し違います.イオン化エネルギーは価電子バンド(電子が詰まっているエネルギー準位の集まり)の上端と真空準位のエネルギー差で定義されます.そのため、仕事関数とはバンドギャップの半分の大きさ分のエネルギー差があります.
金属の仕事関数はおおよそ 2~6 eV 程度の値を持ちます.最小の仕事関数を示すのは Cs(1.93 eV)であり、この点はイオン化エネルギーの傾向と同じです.
仕事関数は表面の電子状態を反映したものなので、表面の原子の種類、形状、面方位、他の原子の吸着度合いによって変化します.例えば、同じ原子同士の場合は、表面に原子が密に並んでいる方が仕事関数が大きいです.
このような外的要因により、同じ種類の試料であっても仕事関数が 1 eV スケールでずれる場合があります.
仕事関数の測定
仕事関数は光電子分光やX線光電子分光法(XPS)によって測定することが可能です.
すなわち、光やX線を試料表面に当てることによって最高エネルギーの電子を叩き出し、入射したもののエネルギー差を測定することで仕事関数を見積もります.
例として光電子分光では、仕事関数は以下の式から算出されます.
ここで、は入射した光のエネルギー、
はフェルミエネルギー、
は仕事関数です.
まとめ
仕事関数は、物質の反応性(安定性)を推察するための極めて基礎的かつ重要な物理量です.表面の影響が多分に現れるため必ずしも一定の値が現れるとは限りませんが、物質間で比較する限りでは有用です.
仕事関数の小さい物質は概して反応性が高く、空気・水と激しく反応するアルカリ金属は顕著な例です.酸化物は安定なため仕事関数が大きい物質が多いですが、というセラミックスは常温・空気中で安定にも関わらず小さな仕事関数の値を持ちます.この小さな仕事関数の値を利用し、
は触媒反応に高い活性を示します.[a,b]
参考文献
pleistoros - Ionization energy and work function
Work Function: Formula & Relation To Threshold Frequency | Electrical4U
[a] Advanced Materials, 2007, 19.21: 3564-3569.
[b] Nature chemistry, 2012, 4.11: 934-940.