更新 2024-2-23
ブラべー格子(ブラベ格子、Bravais lattice)
固体結晶中において、すべての原子は3次元的な周期配列をしています.それゆえ、結晶には最小の堆積の繰り返しユニットが存在し、これを単位胞(単位格子)と呼びます.単位胞で埋め尽くした空間を結晶格子と呼びます.
最も単純な単位胞は平行六面体から構成され、単位胞には結晶の持つほぼ全ての情報が含まれています.例えば、単位胞を見ることで結晶の対称性、原子の位置と原子間距離・角度、密度が分かります.
実際の結晶は膨大な数の原子を含んだ複雑なものですが、単位胞を考えるだけでこれだけの情報が分かるのです.
平行六面体の頂点に当たる点を格子点、格子点の集合体を空間格子と呼びます.結晶格子における原子を格子点で代表させたものを空間格子と考えることができます.
空間格子の繰り返し単位は平行六面体であり、3辺の長さ(a, b, c)とそれらがなす角(α, β, γ)が下図のように定義されます.これらの値を格子定数と呼びます.下図のように、繰り返し単位の頂点だけに格子点を含む場合は単純単位格子と呼ばれます.

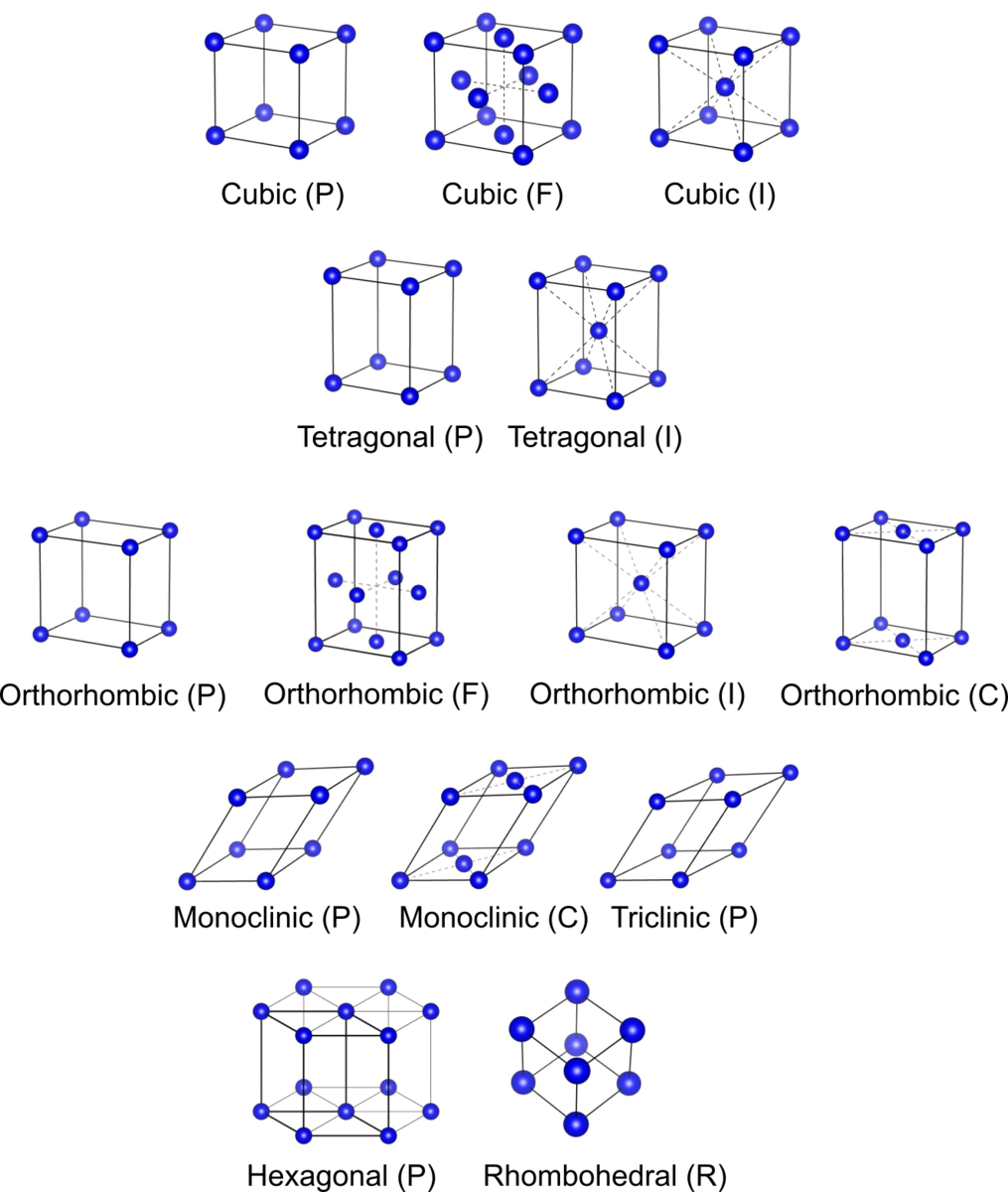
7つの結晶系と14のブラべー格子
| 結晶系 | 格子定数 | ブラべー格子 | |
|---|---|---|---|
| 三斜晶系 | Triclinic |
a ≠ b ≠ c α ≠ β ≠ γ ≠ 90° |
単純(P) |
| 単斜晶系 | Monoclinic |
a ≠ b ≠ c α = γ = 90° ≠ β |
単純(P)、底心(C) |
| 直方晶系 | Orthorhombic |
a ≠ b ≠ c α = β = γ = 90° |
単純(P)、底心(C)、 体心(I)、面心(F) |
| 正方晶系 | Tetragonal |
a = b ≠ c α = β = γ = 90° |
単純(P)、体心(I) |
| 三方晶系 |
Trigonal
Rhombohedral
|
a = b ≠ c α = β = 90°, γ = 120° a = b = c α = β = γ < 120° ≠ 90° |
単純(P)
単純(R)
|
| 六方晶系 | Hexagonal |
a = b ≠ c α = β = 90°, γ = 120° |
単純(P) |
| 立方晶系 | Cubic |
a = b = c α = β = γ = 90° |
単純(P)、体心(I)、 面心(F) |
空間格子は、対称性の観点から7つの結晶系に区分されます.結晶系は上表のように、格子定数に関する条件から区別されます.
数学的には単純単位格子だけを考えれば事足りますが、人間が結晶を解釈する上で単純単位格子だけでは分かりにくいのも確かです.そのため、格子内に複数の格子点を持つ、より大きな格子を採用することで直感的に理解しやすい格子を作ります.
これにより、全ての空間格子は14種類のブラべー格子に区分することができます.
まとめ
今回の内容は、個別の項目で引用するために作成したのでややあっさりです.詳しく知りたい人は成書を参考にしてください.
参考文献
結晶構造の描画にはVESTAを使用.K. Momma and F. Izumi, "VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data," J. Appl. Crystallogr., 44, 1272-1276 (2011).