
更新 2024-2-23
熱膨張とは(Thermal expansion)
固体は温度を上げると膨張します.非常に身近な現象であり、日常生活でも熱膨張を実感することがよくあります.
例えば、台所の流し台にカップラーメンのお湯を流すと「ボコッ」と鈍い音がしますが、これは急激に熱されたステンレスが膨張して反りあがることに由来します.線路のレールには「継ぎ目」があるということを聞いたことがありますね.僅かな隙間を入れることにより、熱膨張によってレールが曲がってしまうのを防ぎます.その分、乗り心地は犠牲になりますが仕方のないことです.
昨今の集積回路は非常に小さな材料を使用しており、どんな小さな熱膨張であっても命取りになります.また、金属やセラミックス、半導体など様々な種類の材料を組み合わせていることから、熱膨張の違いにより破断や断線などが起こる恐れもあります.
一般に、温度差が生じるような環境で使用するような製品は必ず熱膨張を考慮に入れて製造・使用されます.このように書いてしまうと熱膨張は邪魔者でしかないように見えますが、そんなことはありません.役に立つ応用例も数多く存在します.

熱膨張の評価
熱膨張の大きさを評価する係数として熱膨張係数があり、線熱膨張係数と体積熱膨張係数が主に使われます.これらは、温度を上げた際にどの程度伸びるか(線膨張)、どの程度膨らむか(体積熱膨張)を表す係数であり、以下の式で定義されます.
(線熱膨張係数)
(体積熱膨張)
ここで、は線の長さ、
は温度、
は体積を表します.
そのほか、体積当たりの熱膨張を示す体積熱膨張係数などもありますが、あまり使われません.等方的に膨張する物質であれば、の関係があります.3つの次元の方向に等価なので3倍です.
代表的な物質の熱膨張係数を以下に示します.
鉄
ステンレス
アルミニウム
ガラス
エタノール
シリコン
一般的な物質では熱膨張係数は温度にあまり依存しないことが知られています.
鉄を例にとると、温度が1度上昇すると長さが0.001%伸びることになります.100度だと0.1%です.たいしたことないように見えますが、大きな材料であれば深刻な影響を及ぼします.例えば、10 mの鉄線を50度加熱すると、5 mmも伸びます.
線路に隙間を作る理由がわかりましたね.日中の線路はかなりの高温になることもあり、継ぎ目がないとレールが曲がって電車が脱線して大変なことになります.
悪いことばかりのような熱膨張ですが、役に立つ例もあります.例えば、温度計.かつては水銀を用いた温度計が広く用いられました.温度が上がると水銀が熱膨張し、目盛りの位置が変わることによって温度を読み取ります.安全上の理由から水銀はだんだんと忌避され、アルコールを用いた温度計が代わりに用いられるようになりました.
そのほか、熱膨張の使い道としてバイメタルがあります.これは二種類の金属帯を接合した帯状の材料(ストリップ)で、温度を上げる(下げる)と熱膨張の違いからバイメタルが折れ曲がります.温度変化を機械特性に変換できるため、センサーやスイッチとして利用できます.
熱膨張の起源
さて、ここまでマクロな視点から熱膨張を見てきましたが、なぜ熱膨張は起こるのでしょうか.熱膨張の起源に迫るには物質の結晶構造にまでさかのぼる必要があります.
物質中において、原子と原子はイオン結合だったり、共有結合だったり、何らかの結合によって結ばれています.原子はバネのように常に振動し、互いに近づいたり離れたりを絶えず繰り返しています.ここで温度が上昇するとどうなるでしょうか.温度が上がれば原子の運動が激しくなり、低温よりも広い範囲を原子が動き回ることが予想できます.しかし、原子同士をばねのように考えていては熱膨張を説明できません.
具体的に考えてみましょう.
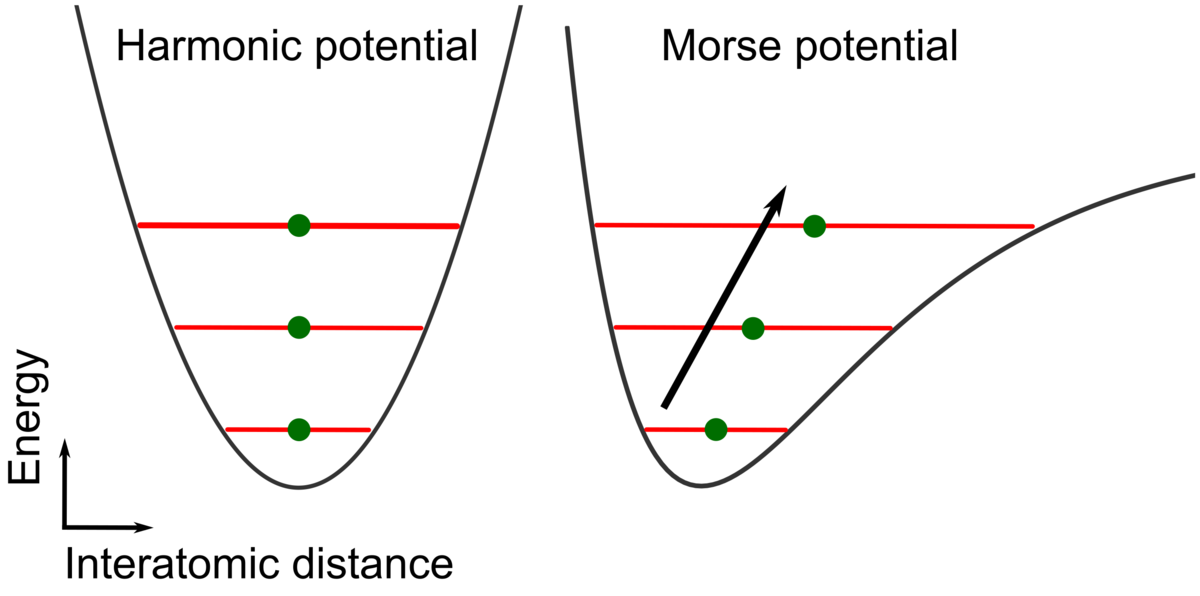
左: (バネ型ポテンシャル)
右:(モースポテンシャル)
一般にバネのポテンシャルは左図のように表されます.高校物理で習った単振動と同じです.原子の変位に比例した復元力が働き、ポテンシャルは二次関数の形になります.
ここで温度を上昇させ、原子を力いっぱい動かしましょう.すると、原子の変位は大きくなりますが、その平均位置は変わりません.ここで指摘しておきたいことは、マクロなものの大きさというのはあくまで原子の平均位置と対応していることです.そのため、原子の重心が変わらないのであれば熱膨張は起こっていないことになります.*1
何が間違っていたのでしょう.実は、原子のポテンシャルを普通のバネで考えたことが間違いでした.実際の原子同士をつなぐバネは、我々のよく知るバネとは異なっており、縮んだ時に押し戻す力と伸びたときに引き戻す力が異なっており、前者の力の方がはるかに大きいことが知られています.
すなわち、右図に示すようなポテンシャルになっています.このポテンシャルを表すためにモースポテンシャルやレナード・ジョーンズポテンシャルなどがよく用いられますが、その言わんとするところは同じです.
例としてモースポテンシャルで原子の熱運動を激しくしてみましょう.多くのエネルギーを与えたとき、伸びる方向にはどんどん進みますが、縮む方向にはなかなか動きません.すると、平均の原子距離は温度上昇とともにどんどん離れる方向に向かうことが分かります.原子距離が伸びるので、マクロな物質も大きくなります.これが、熱膨張の直接的な原因です.
もちろんモースポテンシャルだけで全てを説明することはできませんが、定性的にうまく熱膨張の説明が可能です.なぜ原子は縮むよりも伸びやすいのかという問題もありますが、これにはパウリの排他律が絡んだ複雑な話になってきます.少なくとも、物質は必要以上に近づくことを嫌う性質があるようです.
まとめ
このように熱膨張は固体が当然のように備えている性質です.では、反対に温めると縮むような物質はあるのでしょうか.非常に興味深いことに、そのような物質は存在し「負の熱膨張」物質と呼ばれています.別の記事では、負の熱膨張を示す材料について紹介しています.
*1:平均で考える必要があるのは、物質の中にあまりに多くの原子があるからです.一つ一つの変位を導き出すことは現実的ではありません.